《算法图解》读书笔记3

发表于 | 分类于 | |

《算法图解》Grokking Algorithms （3）

第七章 狄克斯泰拉算法（Dijkstra’s algorithm)

使用

  1. 找出“最便宜”的节点（最短时间或花销最少）
  2. 更新该节点到各个邻居的开销
  3. 重复这个过程，直到每个节点都被考虑到
  4. 计算最终路程

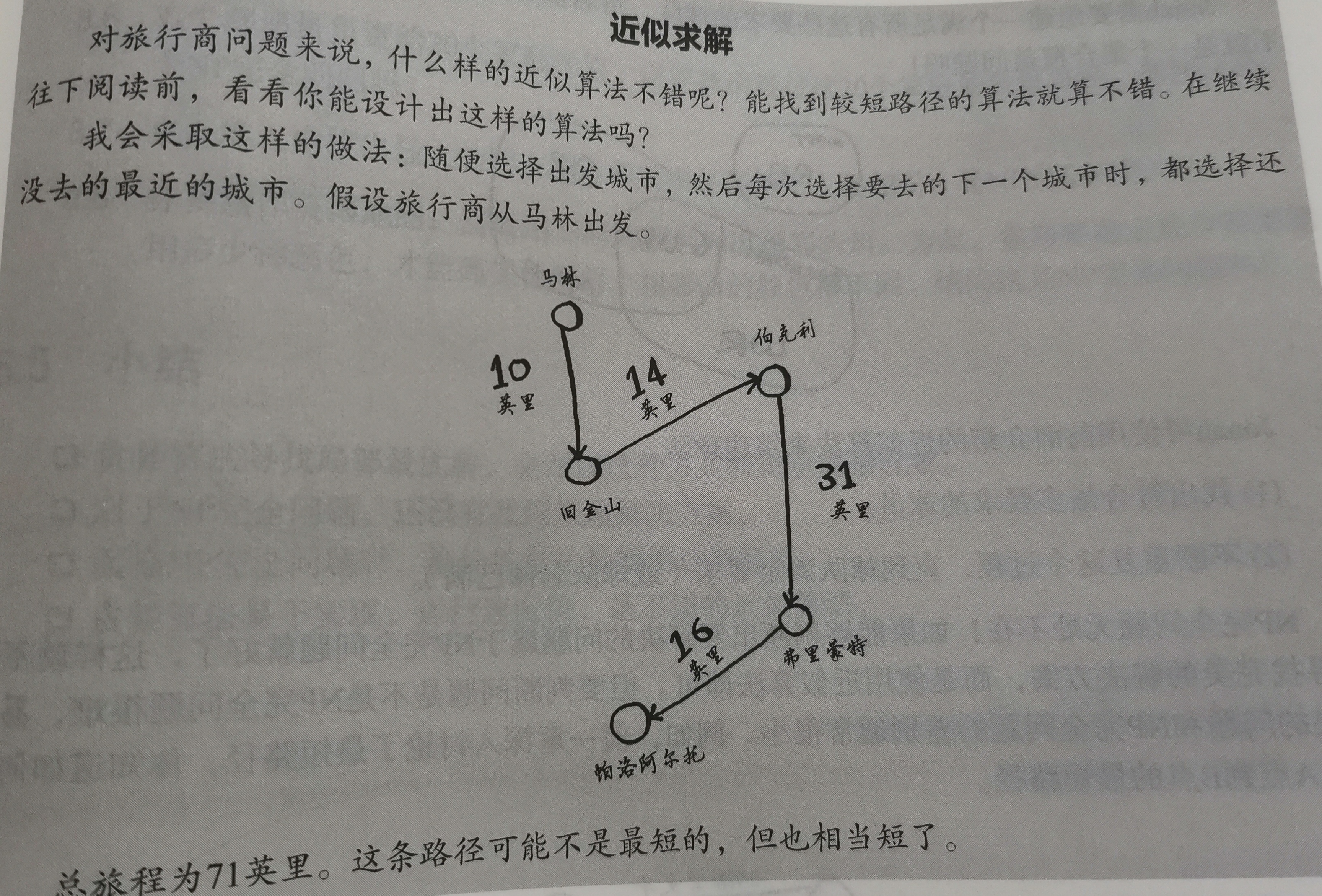
比如：

d1yHPI.jpg

*图上数据为所花时间

如果用上一张所讲的广度优先搜索，所得的结果为从起点到A再到终点，因为段数最少

但是当加上时间权重，我们发现6+1不是最短路程，从起点到B到A在到终点只需要2+3+1=6，这就需要使用狄克斯泰拉算法

步骤：

  1. （找到距离最短的节点）从起点出发，有两个节点，到A要6分钟，到B要2分钟，发现到B所花时间短，于是从B开始找周围的邻居
  2. （从节点找到邻居的开销）从B开始，到A需要3分钟，使用从起点到A的最短时间更新了，为5分钟；从B到终点需要5分钟，所以从起点到终点最短时间更新为7分钟
  3. （需要找全所有节点）再从A开始找，发现从起点到终点最短需要6分钟
  4. 这样所有的点都找齐了

狄克斯泰拉算法与广度优先搜索本质区别就是它有权重

术语

  1. 权重：每一段都有开销，并非以一整段为一个单位
  2. 加权图：每一段都有权重的图（weighted gragh）；非加权图相反（可用广度优先搜索查询最短路径）
  3. 环：从节点出发走一圈回到该节点（即前一章所说的无向图，不适用与狄克斯泰拉算法->可能重复计算一个节点）

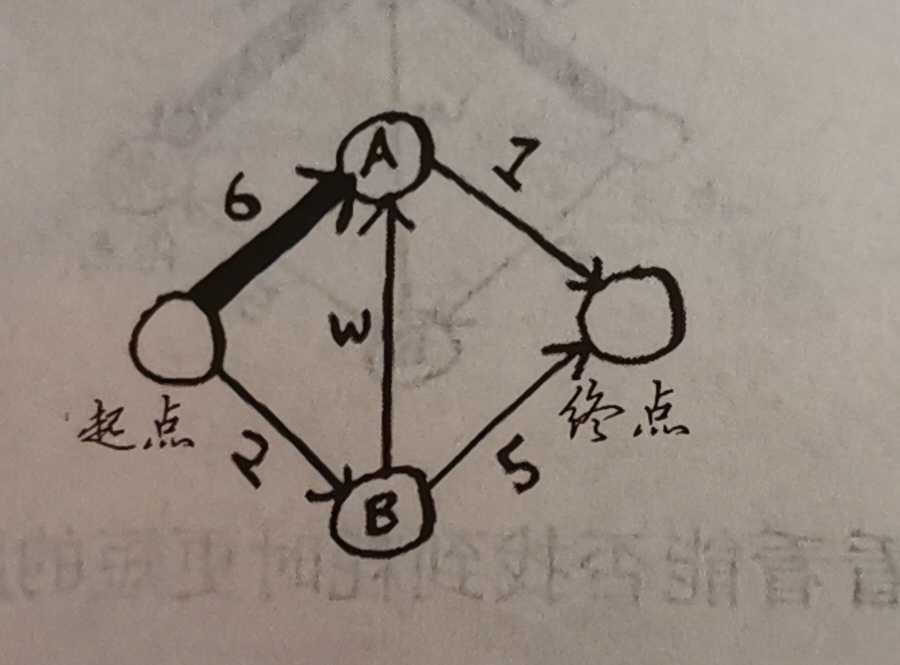
以物换物示例

A：我想用乐谱换你的海报，如果你再加5块我愿意给你我的黑胶唱片

B：我很喜欢那个黑胶唱片，我愿意拿吉他或者架子鼓换

A：我刚好想要个吉他，我愿意用我的钢琴换

d1IdH0.jpg

根据之前的逻辑：

乐谱->黑胶唱片：5

乐谱->海报：0

海报更便宜：海报->吉他：30

海报->架子鼓：35

黑胶唱片->吉他：20（价格更新）

黑胶唱片->架子鼓：25（价格更新）

吉他更便宜：吉他->钢琴：40

架子鼓->钢琴：45

所以最便宜为40

我想到其中有一个问题：为什么海报最低价格为0呢？

从乐谱到黑胶唱片到吉他再回到海报就可以赚20块，即为-20

->改情况不可能存在于狄克斯泰拉算法中，因为该算法每个点只算一遍，不会回头

而出现负数的情况为负权边

考虑到这种情况的另一种算法为贝尔曼-福德算法（Bellman-Ford algorithm）

贝尔曼-福特算法与狄科斯彻算法类似，都以松弛操作为基础，即估计的最短路径值渐渐地被更加准确的值替代，直至得到最优解。在两个算法中，计算时每个边之间的估计距离值都比真实值大，并且被新找到路径的最小长度替代。 然而，狄科斯彻算法以贪心法（贪婪算法）选取未被处理的具有最小权值的节点，然后对其的出边进行松弛操作；而贝尔曼-福特算法简单地对所有边进行松弛操作，共|V|-1，|V|是图的点的数量。在重复地计算中，已计算得到正确的距离的边的数量不断增加，直到所有边都计算得到了正确的路径。这样的策略使得贝尔曼-福特算法比迪科斯彻算法适用于更多种类的输入。贝尔曼-福特算法的最多运行O(|V|*|E|)次，|V|和|E|分别是节点和边的数量）。

伪代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
procedure BellmanFord(list vertices, list edges, vertex source)
   // 该实现读入边和节点的列表，并向两个数组（distance和predecessor）中写入最短路径信息
 
   // 步骤1：初始化图
   for each vertex v in vertices:
       if v is source then distance[v] := 0
       else distance[v] := infinity
       predecessor[v] := null
 
   // 步骤2：重复对每一条边进行松弛操作
   for i from 1 to size(vertices)-1:
       for each edge (u, v) with weight w in edges:
           if distance[u] + w < distance[v]:
               distance[v] := distance[u] + w
               predecessor[v] := u
 
   // 步骤3：检查负权环
   for each edge (u, v) with weight w in edges:
       if distance[u] + w < distance[v]:
           error "图包含了负权环"

实现

用这个例子为准

d1yHPI.jpg

现创建一个散列表：

1
2
3
4
5
graph={}
#从起点可以到A和B
graph["start"]={}
graph["start"]["a"]=6
graph["start"]["b"]=2

添加邻居：

1
2
3
4
5
6
7
8
graph["a"]={}
graph["a"]["finish"]=1

graph["b"]={}
graph["b"]["a"]=3
graph["a"]["finish"]=5

graph["finish"]={}#终点没有邻居

开始时不知道到终点要多久，于是暂时设置为无限大

1
2
3
4
5
infinity=float("inf")
costs={}
costs["a"]=6
costs["b"]=2
costs["finish"]=infinity

现在还需要一个存父节点的散列表

1
2
3
4
parents={}
parents["a"]="start"
parents["b"]="start"
parents["finish"]="None"

还需要一个散列表储存已经查过的点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
processed={}

node=find_lowest_cost(costs)#在所有节点中找出最小开销
while node is not None: #重复到所有节点被找过
    cost=costs[node] 
    neighbours=graph[node]
    for n in neighbours.keys(): #遍历所有邻居的开销
        new_cost=cost+neighbours[n] 
        if costs[n]>new_cost:
            costs[n]=new_cost #如果开销更低，更新开销
            parents[n]=node #设置父节点
    processed,append(node) #将其加入已经操作过的行列
    node=find_lowest_cost(costs) #不断循环
    
def find_lowest_cost(costs):
    lowest_cost=float("inf") #暂时设置最少开销为无穷大
    lowest_cost_node=None #暂时设置没有最便宜节点
    for node in costs: #遍历节点
        cost=costs[node]
        if cost<lowest_cost and node not in processed: #如果有未处理的更低开销节点
            lowest_cost=cost #就设置为最低开销节点
            lowest_cost_node=node
    return lowest_cost_nodec

第八章 贪婪算法

是什么？

例子：安排不同时间的课程

dbPWVA.jpg

此时要选择上更多的课，则可以从最早时间开始：美术、数学、音乐

这就是贪婪算法：每步都选择局部最优解，从而得到全局最优解

虽然不是在任何情况下都行之有效，但它易于实现

背包问题

一个贪婪的小偷，背包可以装35磅的东西，要求将价值最高的商品装入包内

  1. 盗窃可装入包的最贵物品
  2. 再盗窃还可以装入包的最贵物品
  3. 以此类推

但在此情况下就不可行：

有三个物品：音响3000元、30磅，笔记本2000元、20磅，吉他1500元、15磅

如果选择最贵的音响，可以得3000元，为局部最优解

但如果选择笔记本和吉他，可以得3500元

此时贪婪算法不能获得最优解，但非常近似，已经足够使用

集合覆盖问题

有一个广播节目，需要让全美50个州的听众都听到，但每个广播台能覆盖不同的州，不同广播台覆盖区域可能重叠

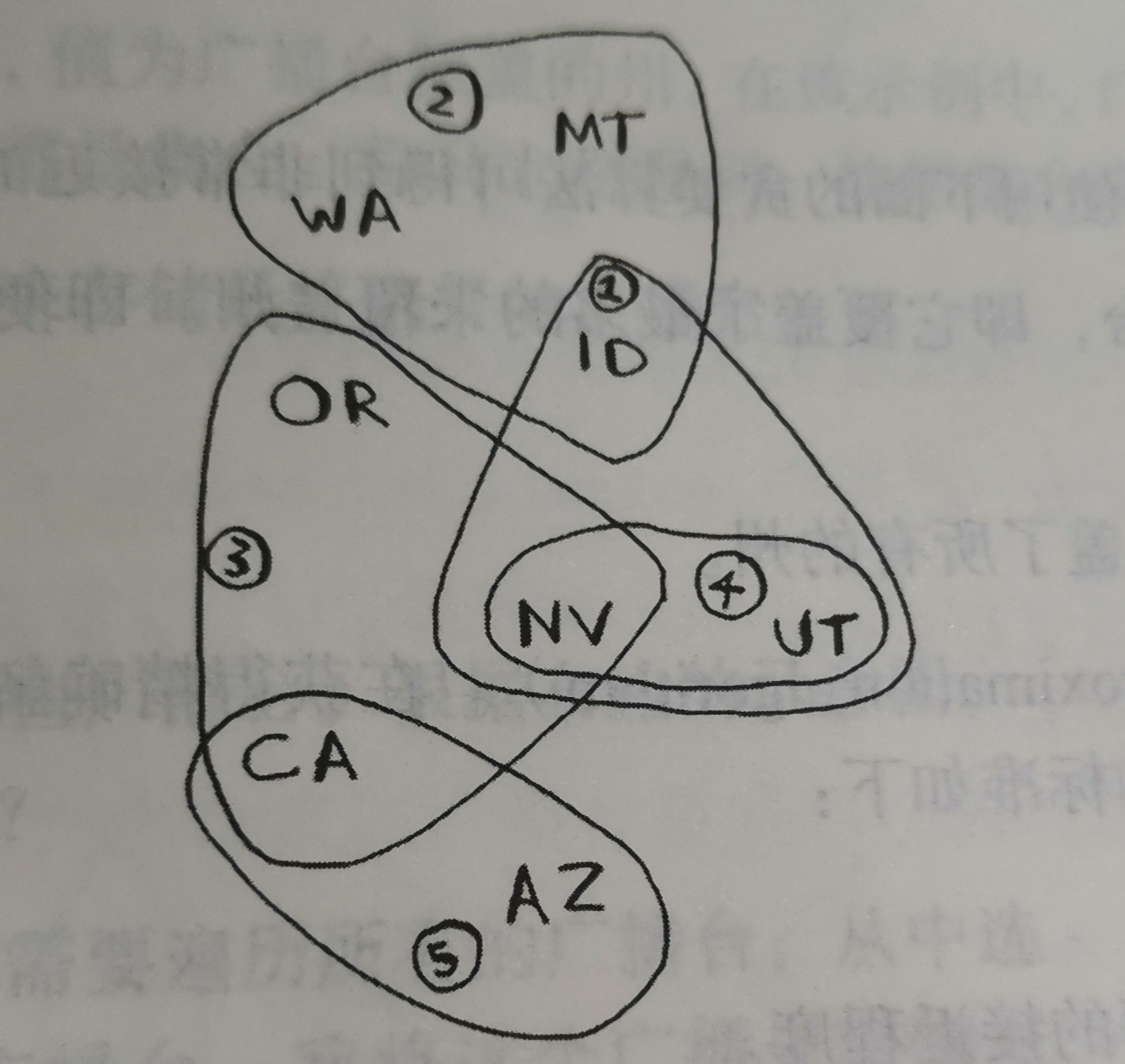
dbiaQS.jpg

怎么找出符合要求的最小广播台合集？

  1. 列出每个可能的广播台合集（幂集power set），可能的子集3有2^n个
  2. 在这些合集里找到最小的合集

这将花费大量时间

贪婪算法可以解决这个问题（近似算法approximation algorithm）

  1. 选出一个广播台覆盖了最多的未覆盖的州（覆盖了已覆盖的州也没关系）
  2. 重复第一步直到覆盖所有州

标准：速度，与最优解相近程度

贪婪算法运算时间：O(n^2) ，n为广播台数量

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
states_needs=set(["mt","wa","or","id","nv","ut","ca","az"]) #需要覆盖的州

stations={}
stations["kone"]=set(["id","nv","ut"])#录入每个广播台可覆盖的州，set将重复出现的州只出现一次
…… #多次录入省略

final_stations=set()#储存最终选择的广播台

#计算：遍历，找到覆盖最多的电台

while states_needed: #不断循环直至所有州被覆盖
    best_station=None
	states_covered=set()
	for station,states_for_station in stations.items():
    	covered=states_needed&states_for_station #找到两者交集
    	if len(covered).len(states_covered): #如果此解更优
        	best_station=station #录入最优解
        	states_covered=covered
    
	final_stations.add(best_station) #加入最终集合
	states_needed-=states_covered #此州已被覆盖

print(final_stations)

NP完全问题

为解决集合覆盖问题，计算每个集合

与第一章所讲旅行商问题类似，全部计算（两地之间往返是两条路）

——>需要计算所有的解，并从中找出最小的那个

此类问题没有快速解决方法，只能用近似求解

dbJGuQ.jpg