《算法图解》Grokking Algorithms （2）

第四章快速排序

divide and conquer(D&C)算法

递归式问题解决方法

理解：

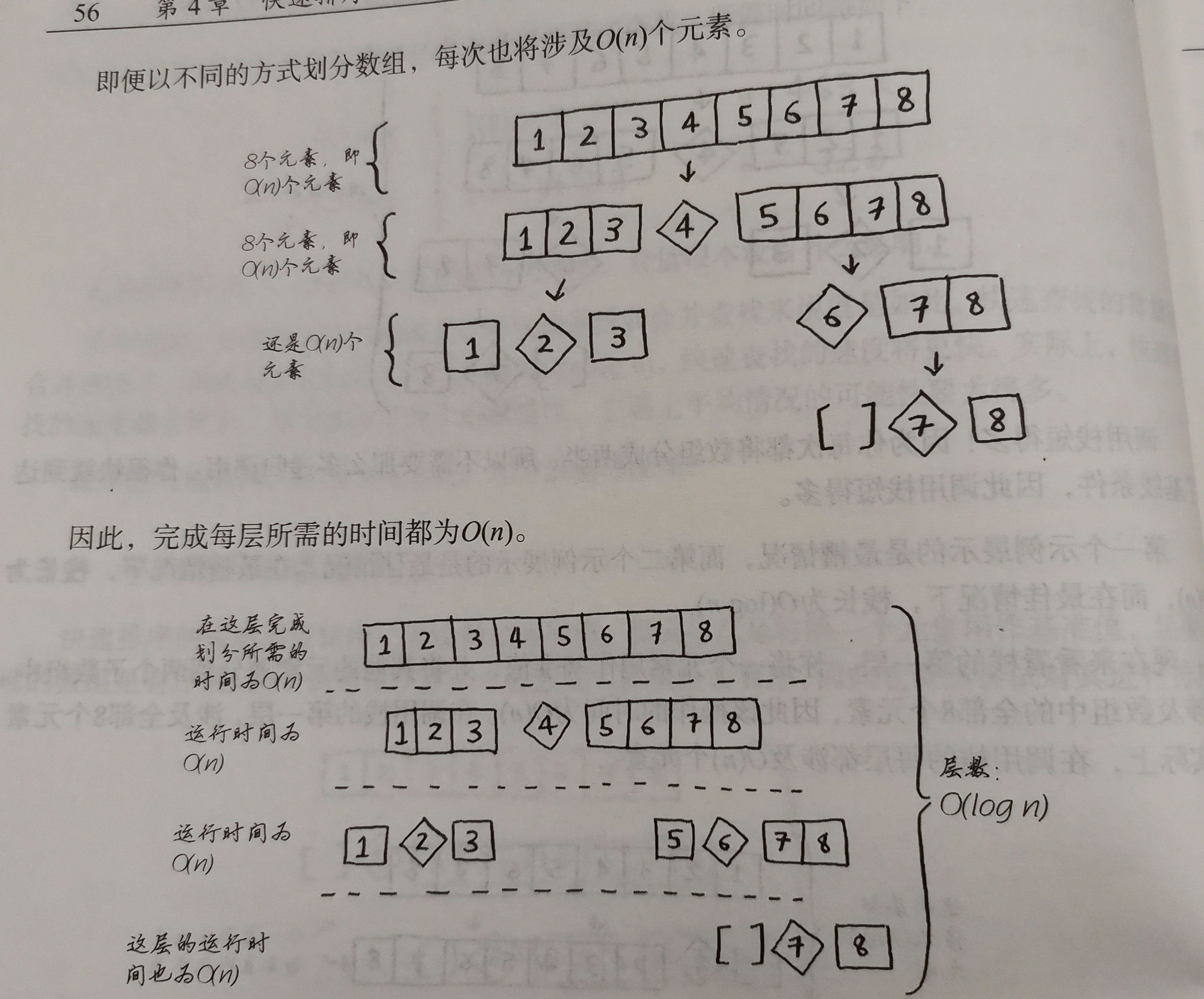
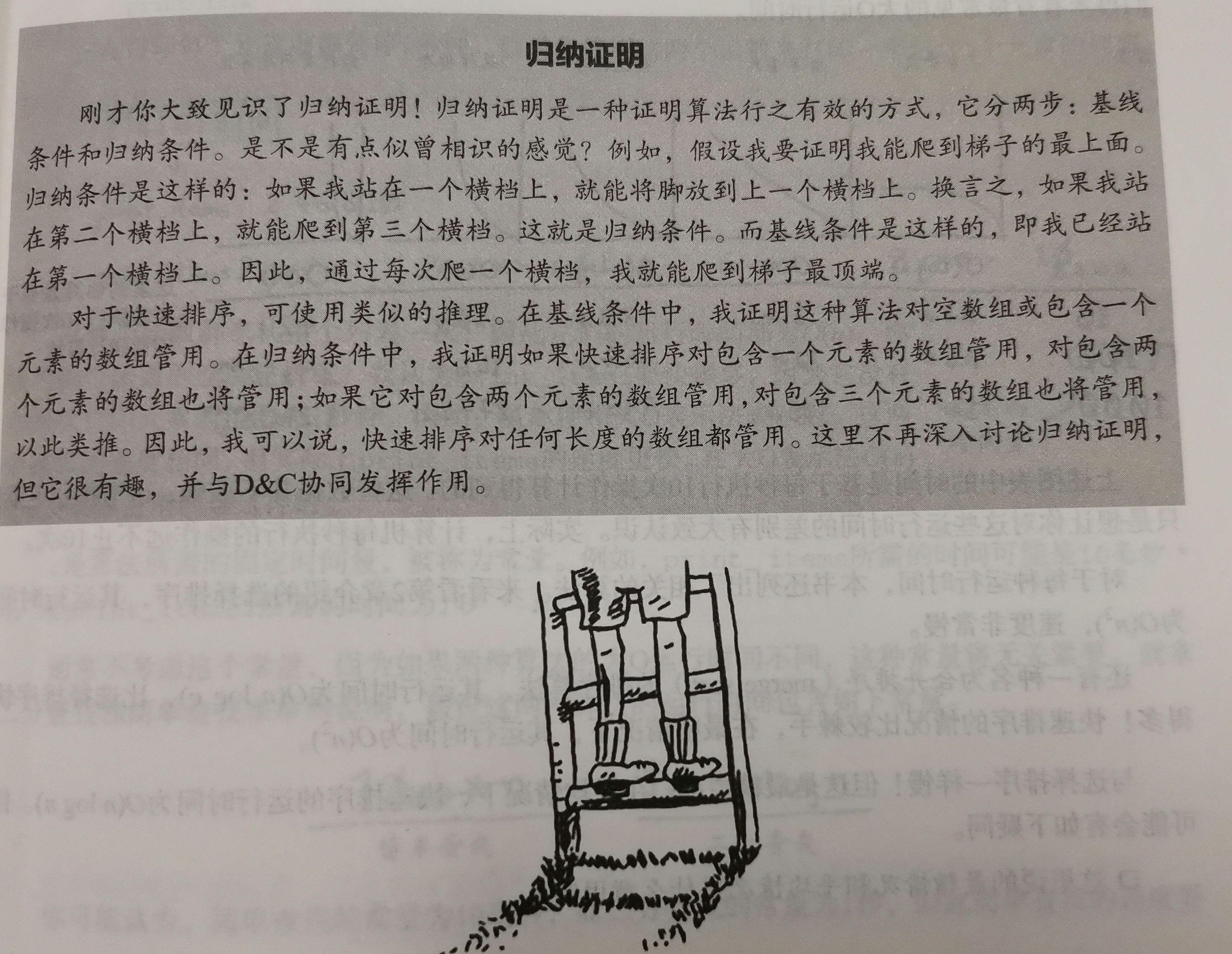
用D&C解决：1）找出基线条件；2）不断分解问题，直到符合

农场主分地，1680m*640m，要求均匀分成正方形，且尽可能大

即一边的长度是另一边的整数倍

在1680640中，1680=640\2+400

即可用640400计算—>问题缩小了（适用于小块地最大方块也适用于整块第的最大方块—*欧几里得算法**）

下面为：640=400+240—>240*400

400=240+160—>160*240

240=160+80—>80*160

160=80*2—>找到了

代码示例：

简单的数列求和：

def sum(arr):
    total=0
    for x in arr:
        total+=x #total+=x 为 total=total+x
    return total

递归法：

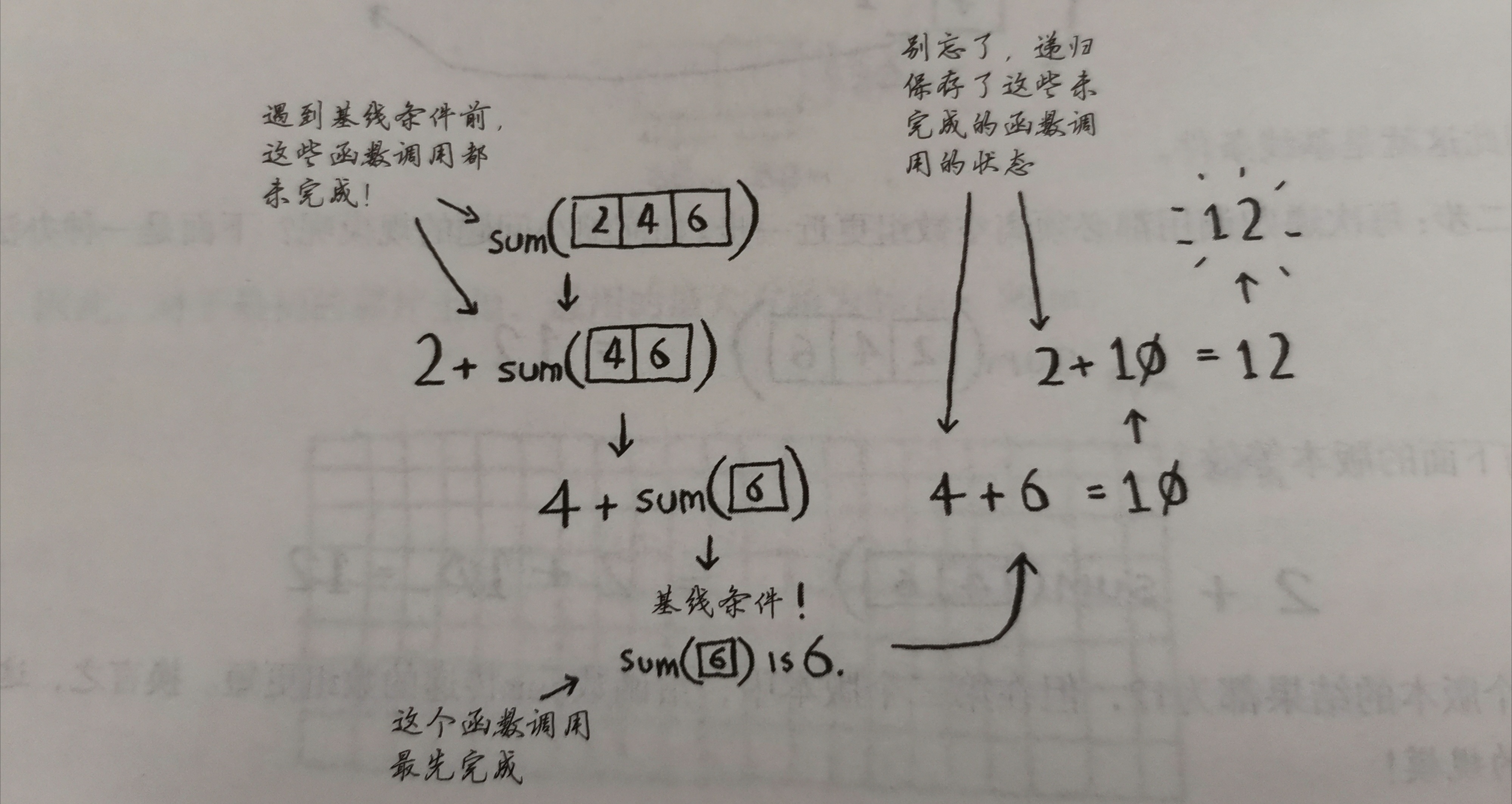
找出基线条件：数组不包含元素或只包含一个元素，计算总和很简单，如数组没有元素，和为0，这就是基线条件
每次递归都要离空数组近一步（缩小问题规模）：

sum（2,4,6）=12 —> 2+sum（4,6）=2+10=12

#连续数字求和
def sum(max):
    if max <= 100 and max >= 0:
        return max +sum(int(max) - 1) #求此时的数与下一个数，max==0为基线条件
    else:
        return 0
print(sum(100))
#out:5050


#列表求和
def list_sum(num_List):
    if len(num_List) == 1:
        return num_List[0]
    else:
        return num_List[0] + list_sum(num_List[1:]) #使用递归直到len(num_list)==1（基线条件）
        
print(list_sum([2, 4, 5, 6, 7]))
#out:24


#找最大值
def max(lis):
    if len(lis)==2:
        return lis[0] if lis[0]>lis[1] else lis[1] #比较一二位大小
    sub_max=max(lis[1:])  #使用递归直到lis只剩两位（基线条件为len(lis)==2）
    return lis[0] if lis[0]>sub_max else sub_max #比较剩下的两个数大小
max([4,2,6,1,9])
#out:9

快速排序

c语言标准库中的函数gsort就是快速递归

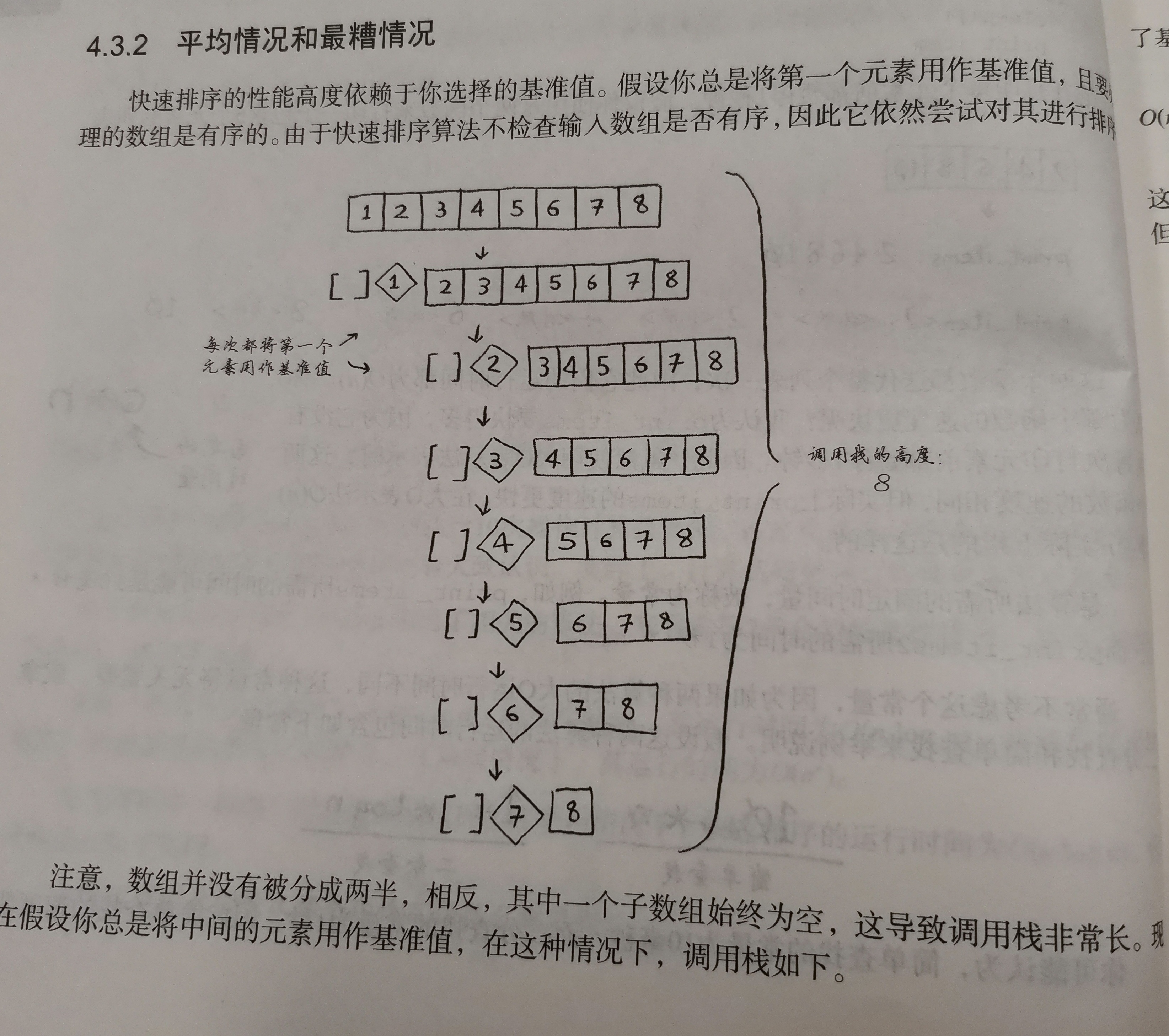
将一个无序的列表排序：将第一个书局当做基准值，将小于它的放前面，大于它的放后面，如：

33,15,10—>（15,10）（33）（）

这被称为分区（partitioning）

现在有三个组，再分别将小于和大于基准值的子数组用相同的方法排序

代码示例：

def quicksort(array):
    if len(array)<2: #如果只有一个值，返回
        return array
    else:
        pivot=array[0] #设置基准值
        less=[i for i in array[1:] if i <=pivot] #取小于基准值的值
        
        greater=[i for i in array[1:] if i >pivot] #取大于基准值的值
        
        return quicksort(less)+[pivot]+quicksort(greater)
    
print(quicksort([10,5,2,3]))
#out:[2, 3, 5, 10]

大O表示法

快速排序速度取决于基准值，速度可以等于合并排序（merge sort），时间为O（nlogn），但糟糕的情况可能跟选择排序（O（n^2））相同。

比较合并排序与快速排序

def print_items(list):
    for item in list:
        print(item)   #10毫秒*n

from time import sleep
def print_items(list):
    for item in list:
        sleep(1)
        print(item)   #1秒*n

两者的大O相同，虽然两者运行时间不同

其中的10毫秒和1秒为c(常数，固定时间)

平均情况和最糟情况

第五章散列表

是什么

在商店的价目表查询商品价格：

无序价目表：简单法（第一章）O=O(n)

按字母顺序排：二分法（第一章） O=O(log2n)

但是店员却能背下价目表，在提及商品时瞬间找到价格：

实现这一点需要散数列

散数列：将输入映射到数字

满足要求：必须一致：当输入一样时输出也必须一样

不同的输入映射到不同的数字：输入不同时输出也不同

==>数学的one to one 函数

步骤:

创建空数组

填写数组：将apple设置为3，则3的元素填写苹果的价格（以此类推）

有用原因：

1.相同输入映射相同索引

2.不同输入映射不同索引

3.散数列知道数组有多大，只映射有效值

可以用字典实现：

book=dict()
book["apple"]=0.6
book["milk"]=1.49
book["avocado"]=1.49
print(book)
#out:{'avocado':1.49,'apple':0.67,'milk':1.49}

实际应用

电话簿查询

网址查询（转为IP地址）：Google.com->74.125.239.133（DNS resolution）

防止重复

在投票时，判断这个人是否已经投过票

设置一个字典，将投过票的人放入字典：

1
2
3

voted={}
#加入投票者姓名
value=voted.get("tom")

如果tom投过票就会出现在这个字典中。返回值为true，否则为false

如果为false（不在列表里）

voted={}
def check_voted(name):
    if voted.get(name): #有名字，即为true，所以此if会执行
        print("had voted")
    else:
        voted[name]=True #将投票者加入这个dict
        print("let them vote")

将散列表用作缓存

网站的缓存

访问网页：（拿百度举例）

向百度服务器发出请求
服务器处理，生成网页发给你
你获得网页

推荐功能：

获取你最近的足迹，推荐你可能感兴趣的内容，即在第二步进行一些运算

但这个过程可能需要几秒，并且它的用户千千万，所花费时间较长。

于是你觉得加载慢，于是你会觉得百度慢、百度这个软件不好

解决：

比如家里一个孩子很喜欢星球，总问你火星离地球多远？月球呢？… …

每次你又要上网搜，在说出答案，这需要花时间，就跟之前网站服务器在第二步运算的时间一样

但问多了你就能记住，月球离地球238,900英里这个答案

下次他再问你你就不需要查

好处：

时间短

网页服务器工作量少

这些缓存就存在散列表中（如主页，about等）（历史记录或者网站缓存里）

实现代码：

cache={} #h缓存的散列表
def get_page(url):
    if cache.get(url):
        return cache[url] #如果有缓存，返回缓存数据，瞬间完成
    else:
        data=get_data_from_serve(url)
        cache[url]=data #将数据保存到缓存里
        return data

这样也可以解释为什么我们第一次访问一个网站的时候要花几秒，但我们访问常用的较大的网站，如百度主页，就会瞬间完成

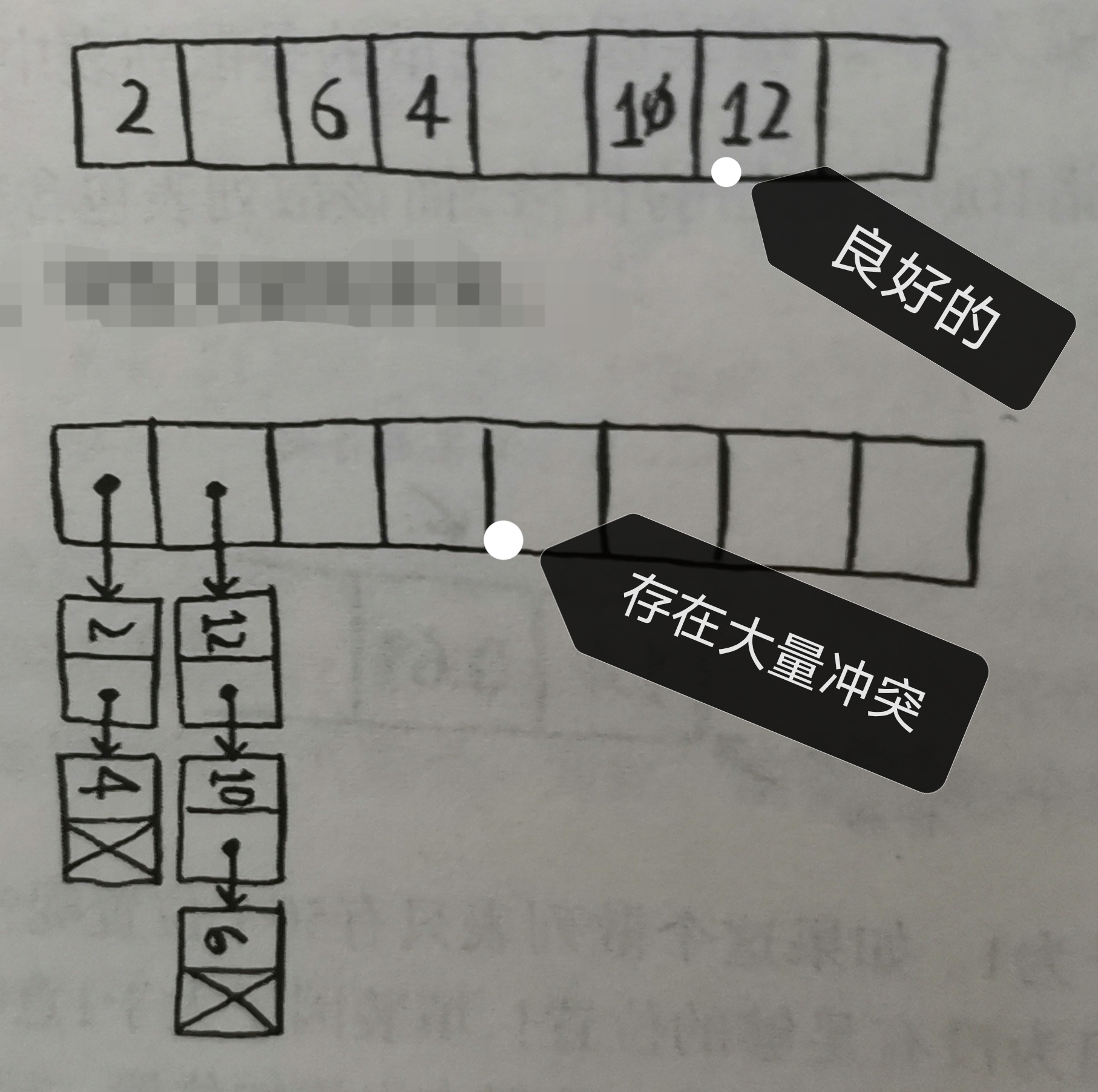
冲突

散列表要做到不同输入映射到数组的不同位置几乎是无法完成的

比如：

将价目表按字母顺序放进散列表：

apple放进第一个，banana放进第二个，但遇到avocado的时候，发现它的首字母也是a

这个时候，覆盖apple，下次查询apple的价格时查到的是avocado（因为这个是数组而不是链表，无法直接在中间加值）

解决方法：在a的位置储存一个链表，将a开头的都放进链表里，但这将使速度减慢

但是，假设这个商店只销售a开头的商品，数组的第一位将特别长，但后面25位将被浪费

需要合理安排散列函数，均匀分配

性能

平均情况：均匀分配列表，获得数组的查找效率和链表的插入删除效率

最糟情况：出现严重冲突，获得数组和链表的缺点

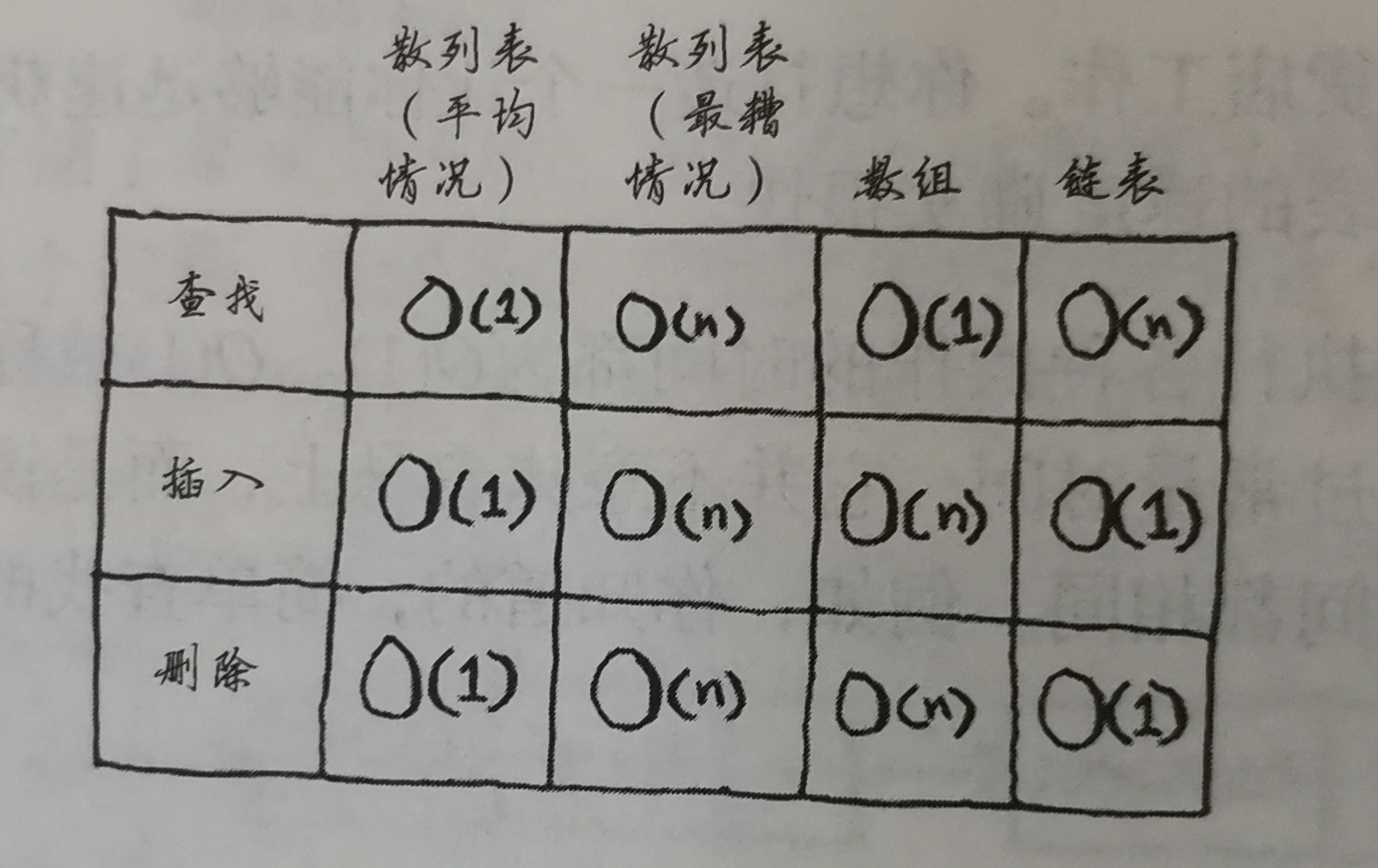
获得平均情况：较低的填装因子，良好的散列函数

填装因子

填装因子=列表包含元素量÷位置总数

如果元素量大于总位数（即需要链表），填装因子大于1，就需要增加数列长度（创建一个新的数列，用hash函数将旧数列的元素装到新数列里），一般填装因子超过0.7就需要调整数列。

良好的散列函数

即均匀排布

第六章广度优先搜索

即找出两样东西之间的最短距离（不一定是指长度上的距离）

图简介

从双子峰做公交去金门大桥：

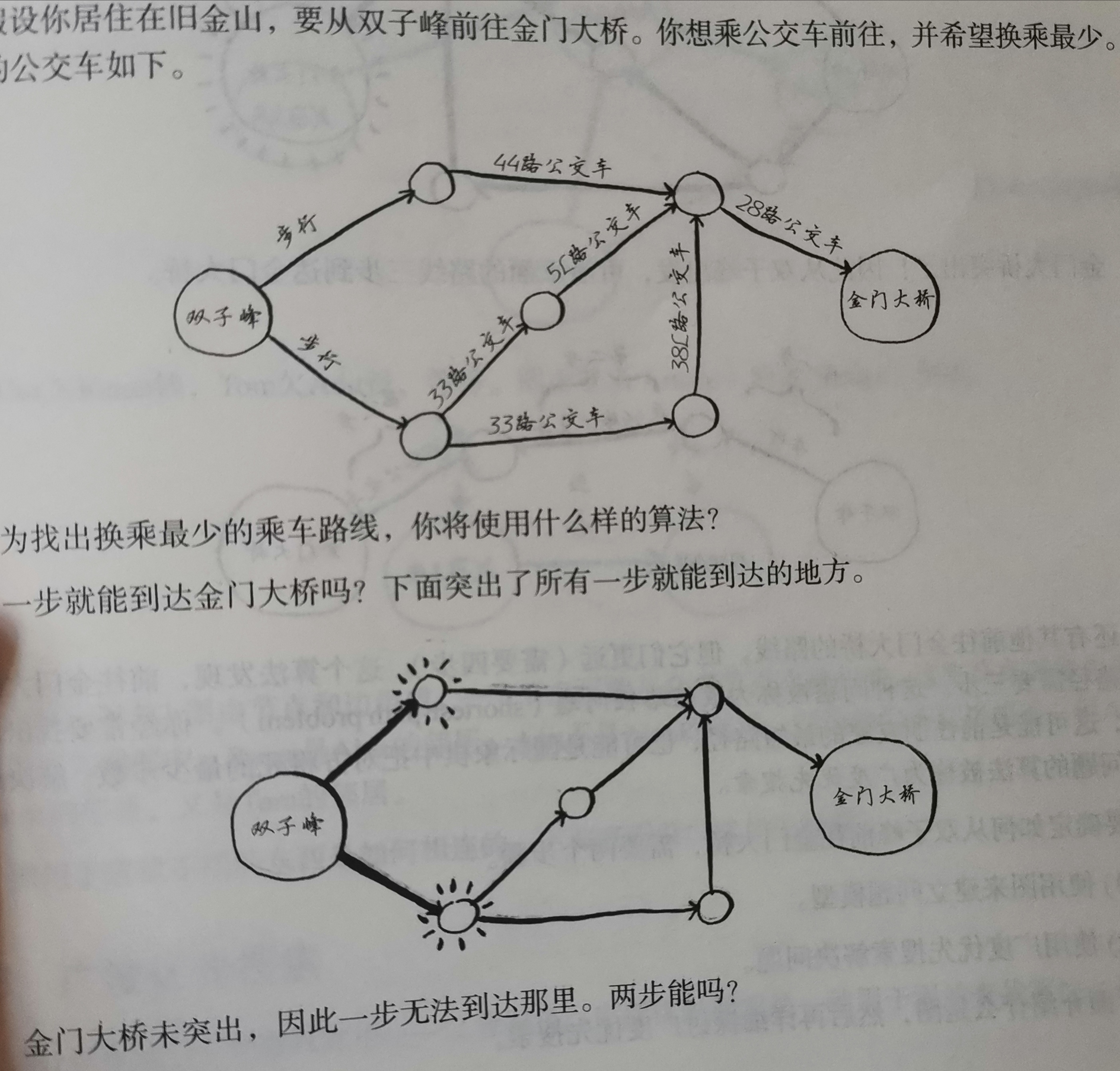
各种地图软件就是这么实现的

图是什么

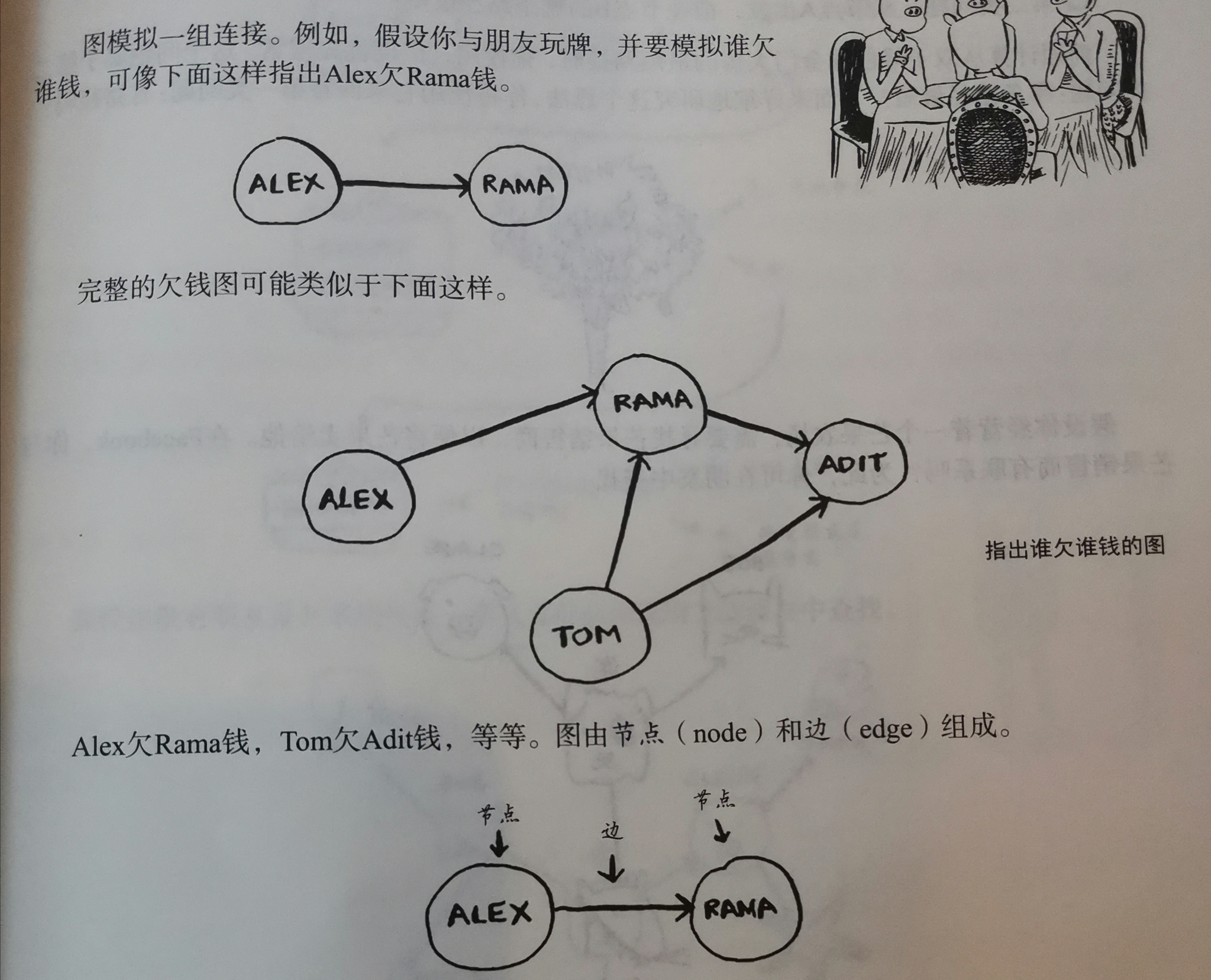
即关系网

广度优先搜索

可解决问题：

从A出发有前往B的路径吗？
从A出发前往B哪条路最短？

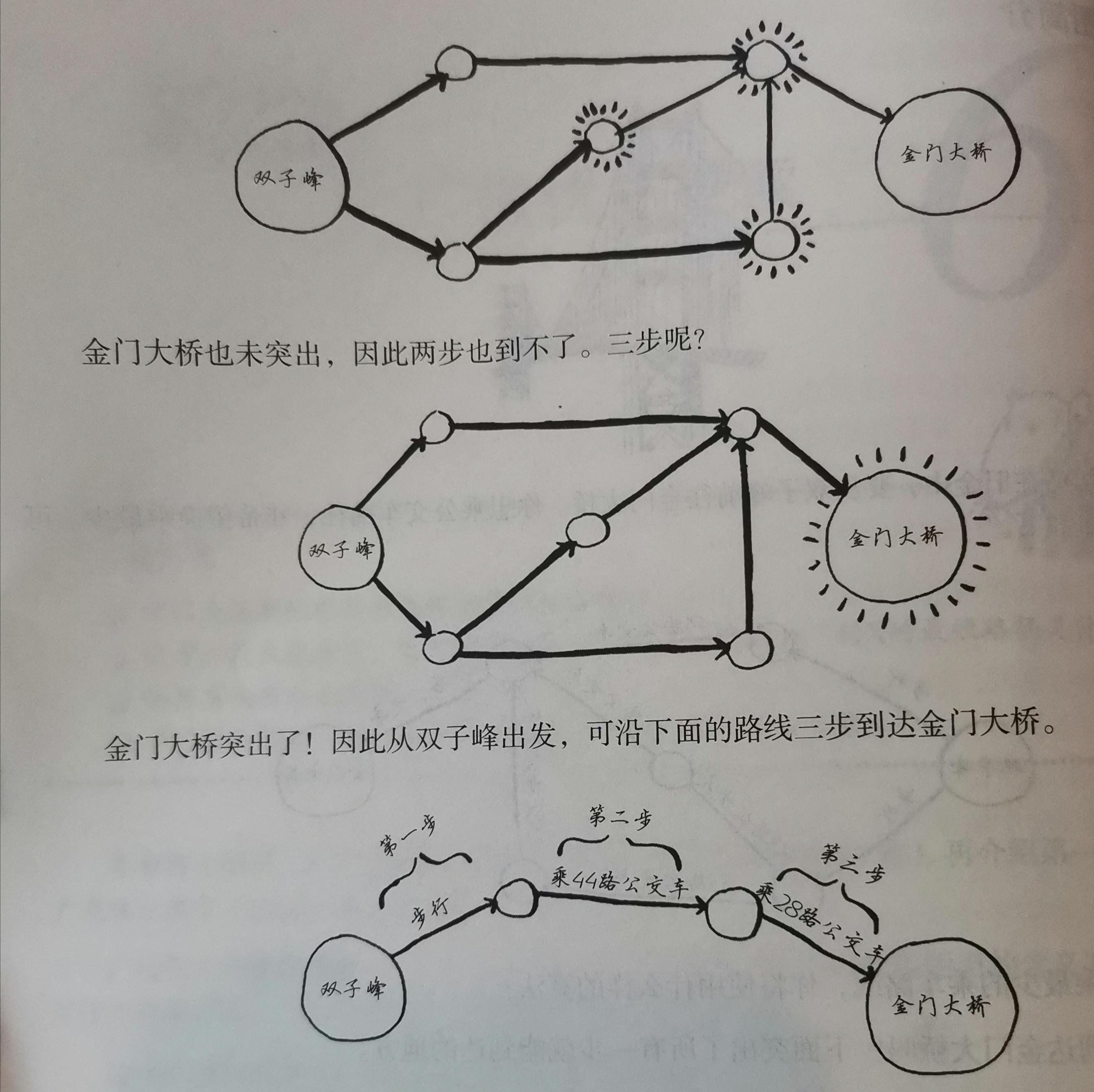
从双子峰去金门大桥的问题即第二个问题

第一个问题：

你有一个农场，你需要一个销售商将商品售卖到市场上

你需要在你的朋友中找有没有销售商

创建朋友名单，再依次检查是否有销售商

但如果你的朋友中没有销售商，你需要在朋友的朋友中找销售商检查每个人时，要将他的朋友加入名单

搜遍你的人际圈直到找到销售商就是广度优先搜索

查找最短路径

第二个问题：谁是关系最近的销售商

第一层关系肯定大于第二层，第二层肯定大于第三层… …

广度优先搜索：先检查第一层关系，全部检查完再检查第二层关系

所以，这不仅是找到路径，还是找到最短路径

这样查找时必须按顺序排名单

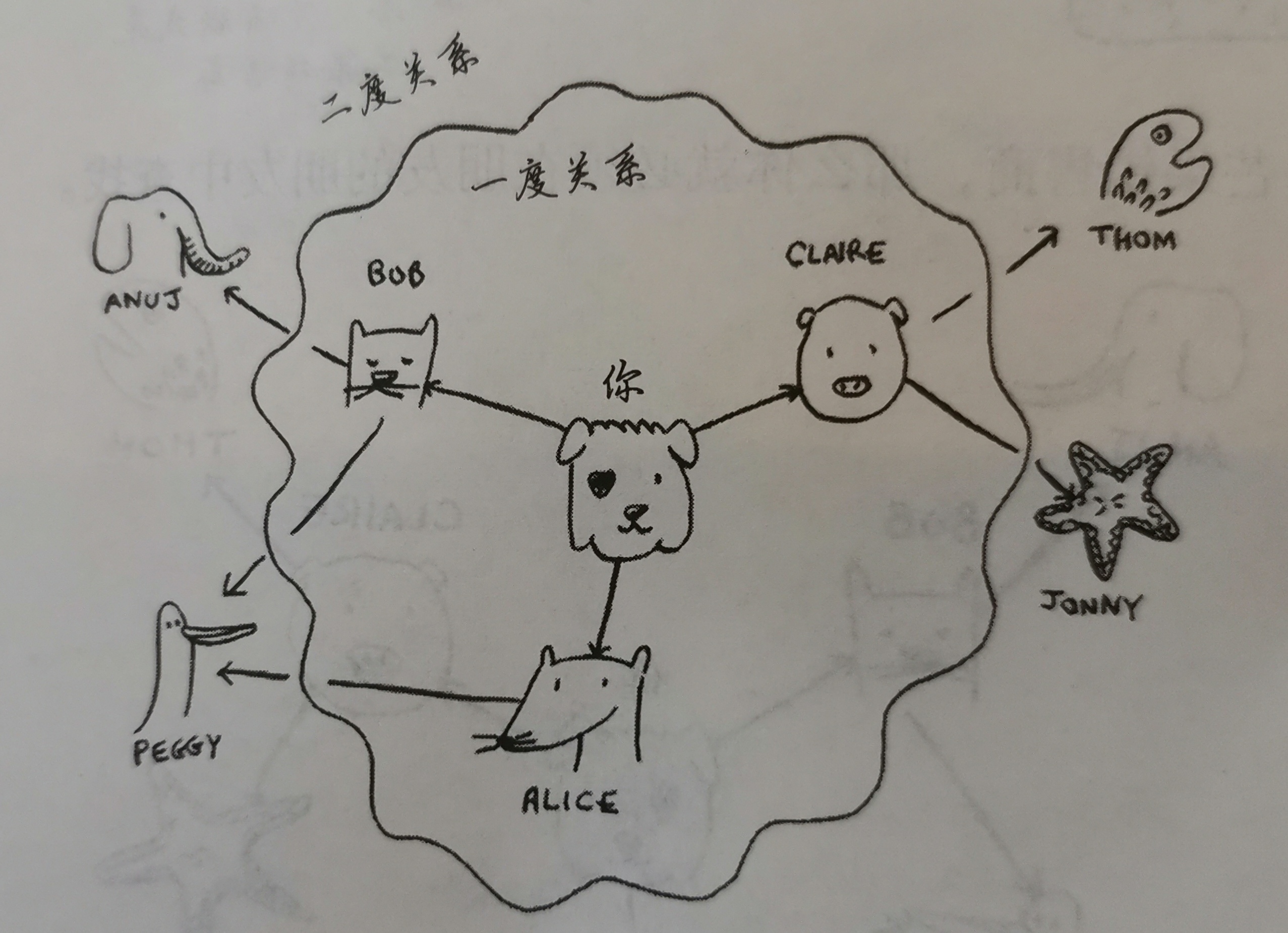
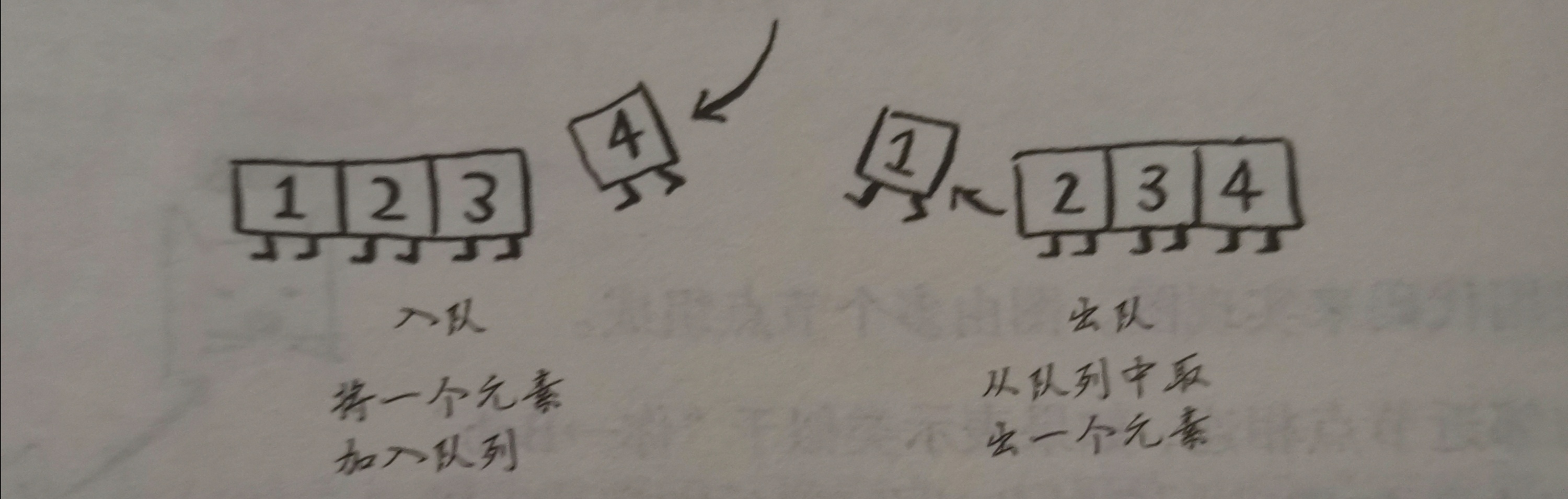
队列

入列和出列

实现图

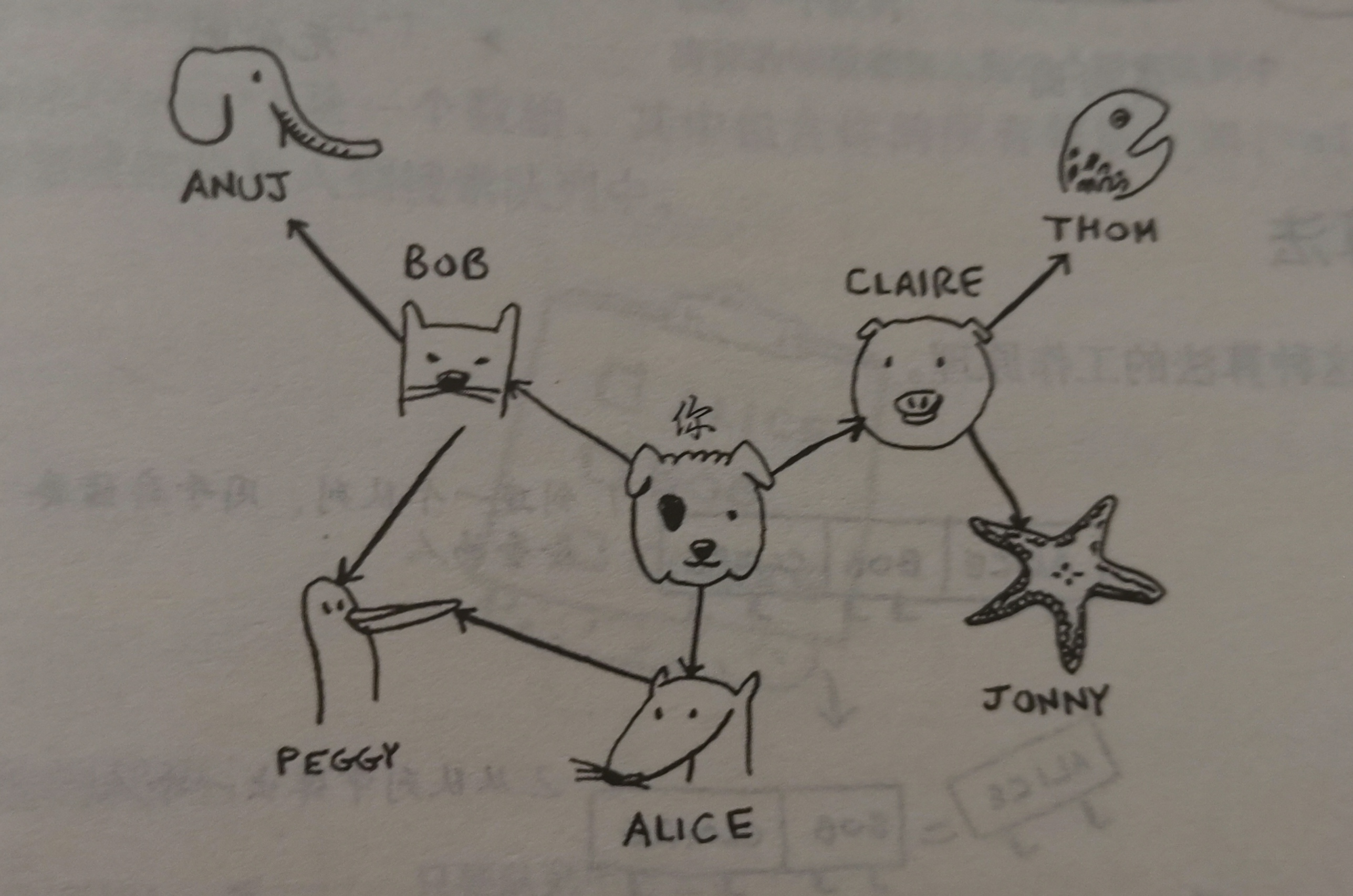
此关系可表示为：

graph={}
graph["you"]=["alice","bob","claire"]
graph["bob"]=["anuj","peggy"]
graph["alice"]=["peggy"]
graph["claire"]=["thom","jonny"]
graph["anuj"]=[]
graph["peggy"]=[]
graph["thom"]=[]
graph["jonny"]=[]

其中代码顺序变化是无所谓的，因为散列表是无序的

这幅图中出现了有向图与无向图：

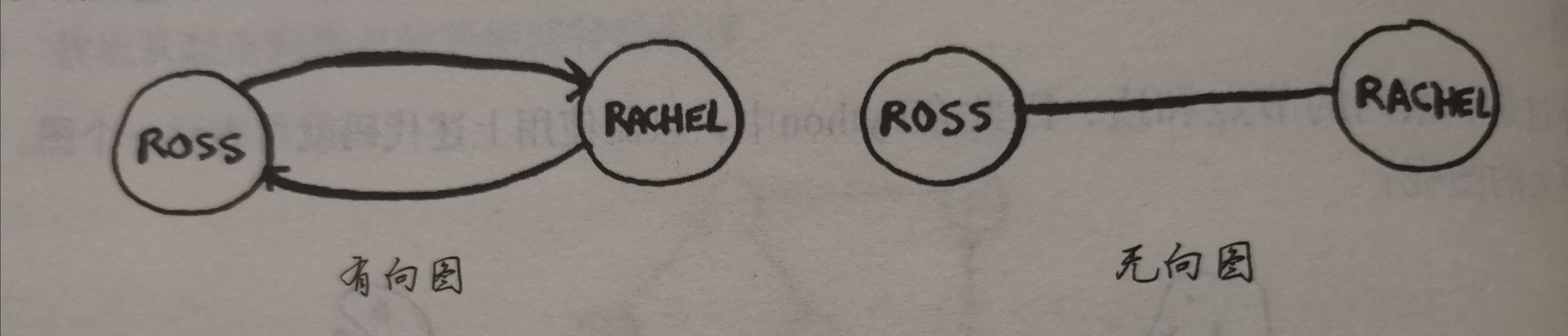
这两个是等价的

实现算法

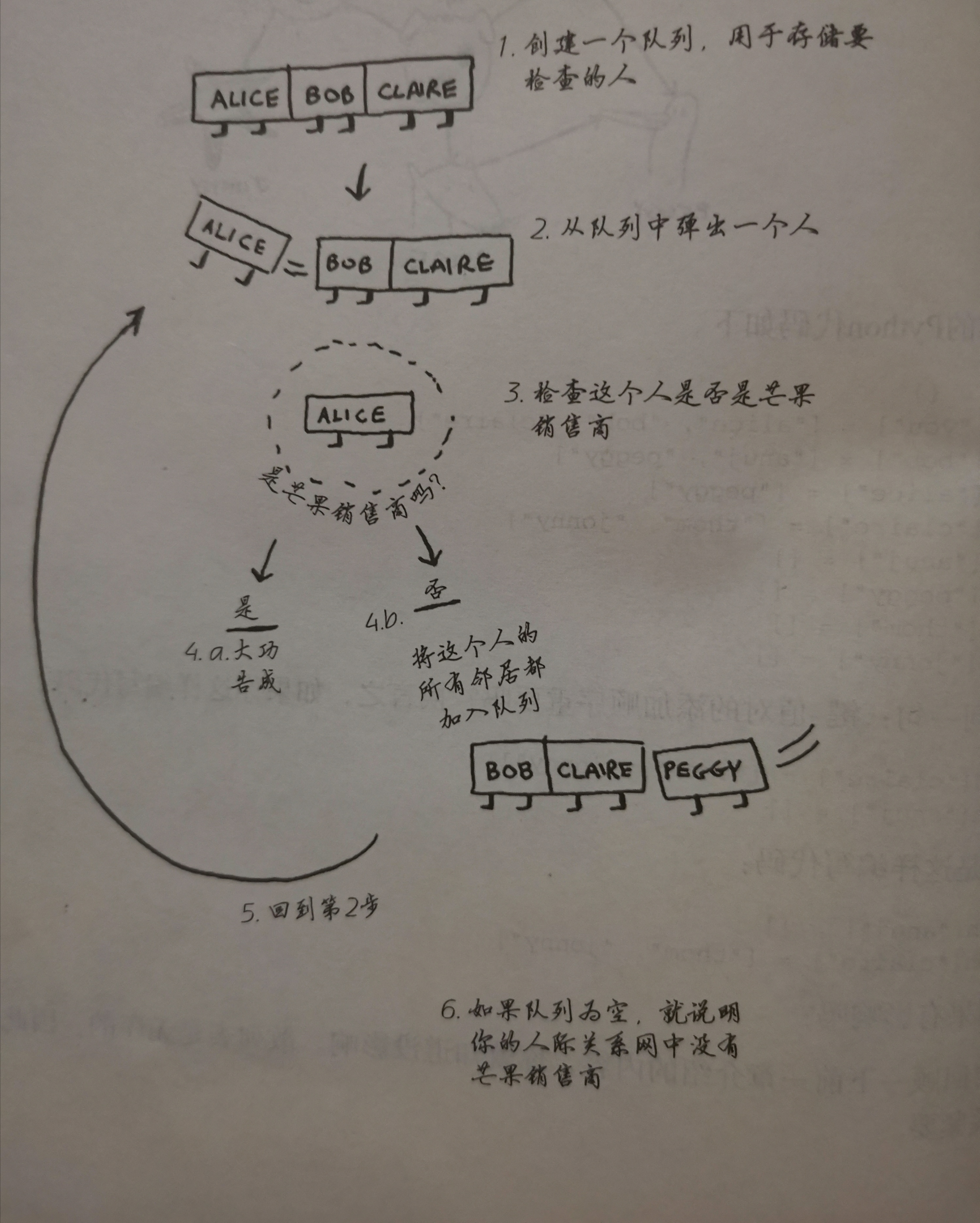
代码：利用deque函数

from collections import deque
search_queue = deque()
search_queue+=graph["you"]#将你的邻居都加入到这个搜索列表

while search_queue:
    person = search_queue.popleft() #从中取出一个人
    if person_is_seller(person): #检查是否是销售商
        print(person+" is a seller!") #是销售商
        return True
    else:
        search_queue+=graph[person] #不是销售商，把他的朋友都加入列表
return False #没有销售商

def person_is_seller(name):
    return name[-1] =='s' #这个人是销售商

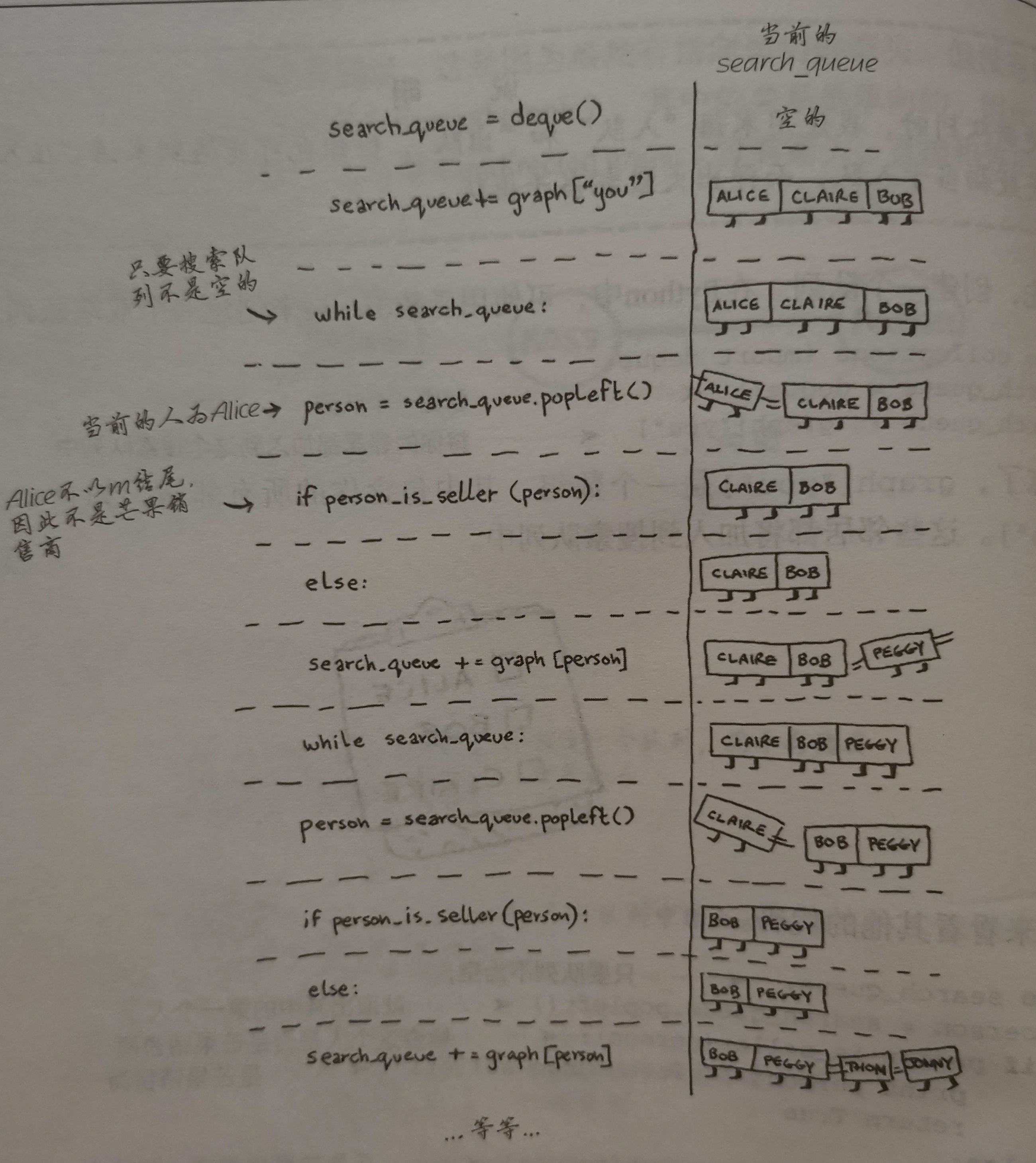
防止死循环出现：

当检查 you这个列表，找到peggy，peggy不是销售商，列出peggy的朋友，peggy的朋友是你，又检查you这个列表… …

所以我们需要加上：

def search(name):
    search_queue=deque()
    search_queue+=graph[name]
    searched=[] #记录检查过的人
    while search_queue:
    	person = search_queue.popleft() #从中取出一个人
        if person not in searched:
    		if person_is_seller(person): #检查是否是销售商
        		print(person+" is a seller!") #是销售商
        		return True
    		else:
        		search_queue+=graph[person] #不是销售商，把他的朋友都加入列表
return False #没有销售商

def person_is_seller(name):
    return name[-1] =='s' #这个人是销售商

search("you")

运行时间

O=O(人数+边数) （可写为O(V+E))