《算法图解》Grokking Algorithms （1）

第一章算法简介

二分法 dichotomy

definition：输入为有序的元素列表，若要找的元素存在，则返回其位置，否则返回null

e.g. 1~100中找数字问题：猜测后会说大了，小了。

简单法查询：从1开始往上猜（至多99次）

二分法查询：50（小了，即可排除一半的数据），75（大了），… … (至多7次)

——大大缩短时间

当数据量加大：

简单法：至多240k步

简单法：

240k—120k—60k—30k—15k—7.5k—3750—1875—937—468—234—117—58—29—14—7—3—1==>17步

结论：对于n项：简单法：至多n步

二分法：至多log2n步

查询代码：(python)

def binary_search(list,item):
    low=0
    high=len(list)-1 #the last value in the list
    
    while low<=high:
        mid=(low+high)/2 #the middle of the whole list
        guess=list(mid)  #check whether the value is correct
        if guess==item:  #find the item
            return mid
        if guess>item:   #find again with deleting the other half of the list
            high=mid-1
        else: 
            low=mid-1
     return None         #item is not in list

大O表示法

O 用来表达运算速度，但不是时间

如：简单法的O = O(n)

二分法的O = O(log2n)

O后所跟的数据为最糟糕的情况

算法运行时间以不同速度增加：

假设一个运算要在10秒内完成，检查一个元素要1毫秒。

如果有100个元素要检查：简单法（100毫秒），二分法（检查7个元素，即7毫秒）

此时简单法是二分法的约15倍

实际有10亿个元素需要检查，二分法需要30毫秒（log2 1 000 000 000），简单法需要二分法的15倍即450毫秒？在10秒之内，可以选择？

不是。简单法需要10亿毫秒，相当于11天

理解不同O的运算时间

在纸上画16个格子：简单法：画16个格子——16步

二分法：将纸对折——4次

常见的大O运行时间

O(log n) 二分法，对数时间

O(n) 简单法，线性时间

O(n*log n) （第4章讲解，较为快速）

O(n^2) （第二章讲解，比较慢）

O(n!) 旅行商问题：非常慢

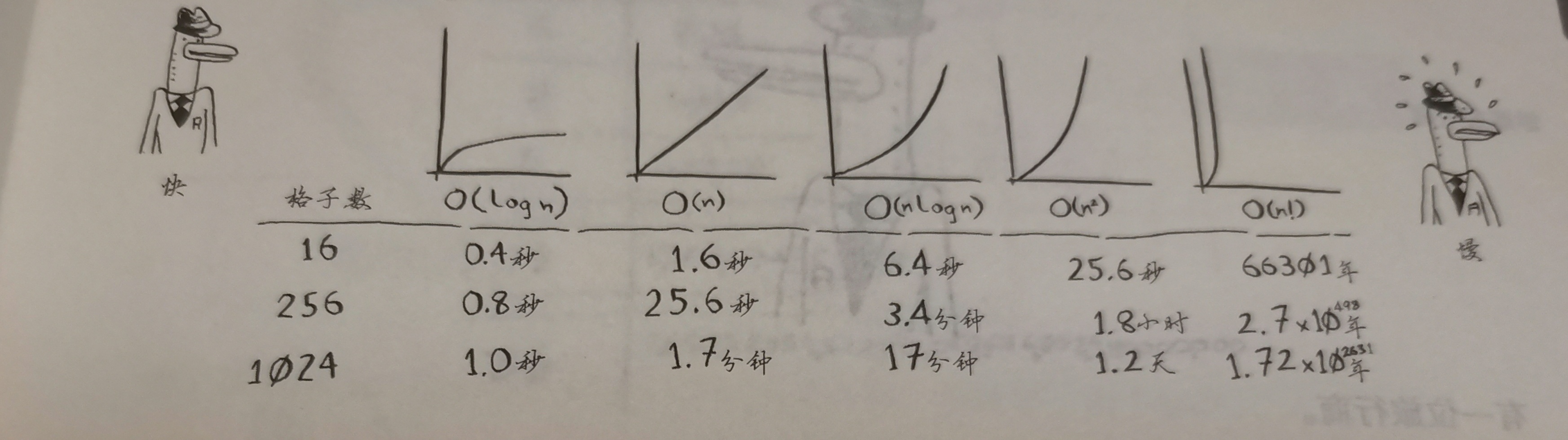
旅行商问题

O(n！) : 运行时间如此长，意义何在？

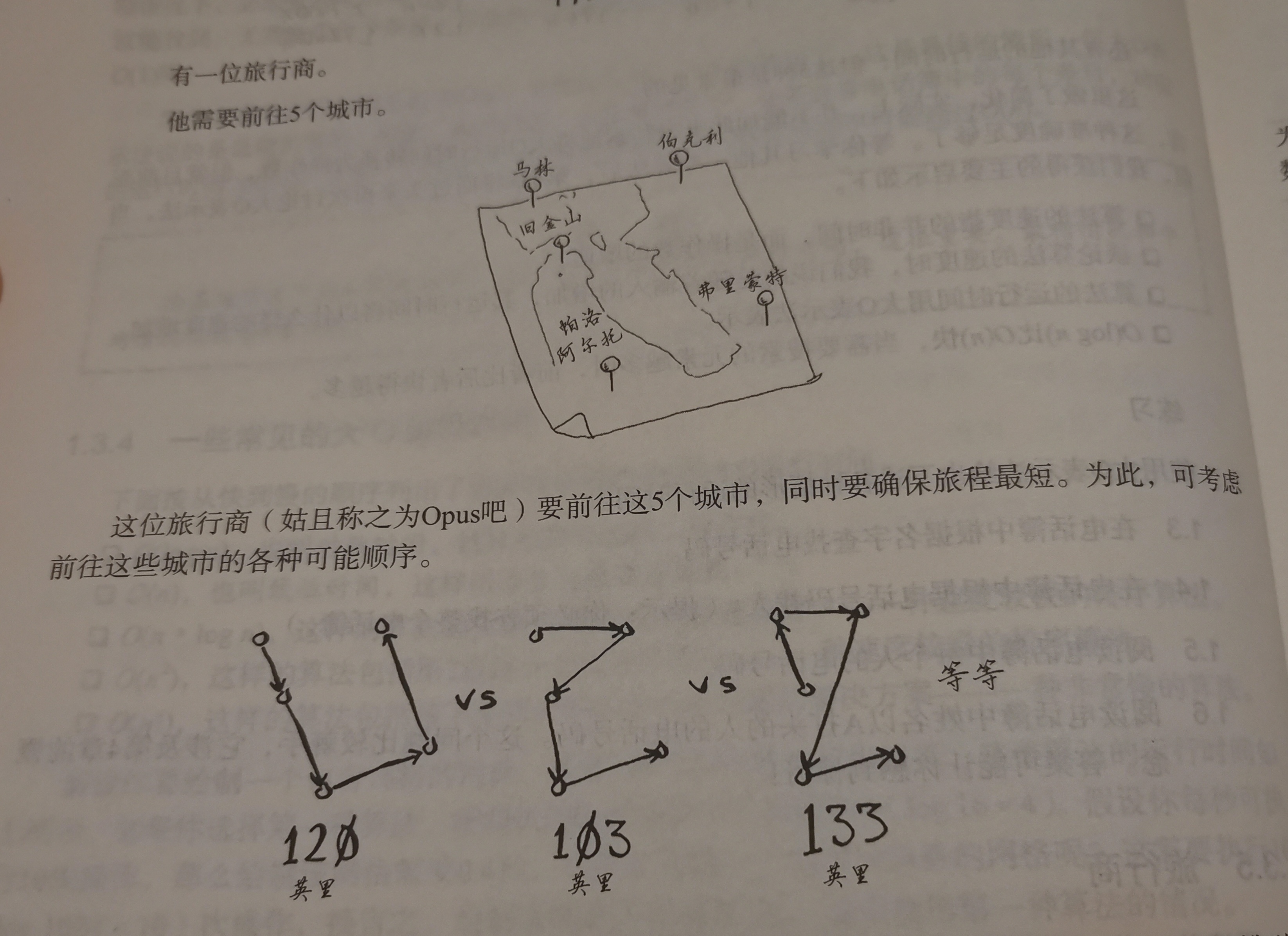
5个城市就有5！=120种方法，6个有720种，7个有5040种… …

尚未有简便算法（可取近似值，详见第10章）

第二章选择排序

内存工作原理：许多可以装数据的小抽屉的集合，每个小抽屉都有地址

数组和链表

储存代办事件：数组or链表？

数组更为简单：

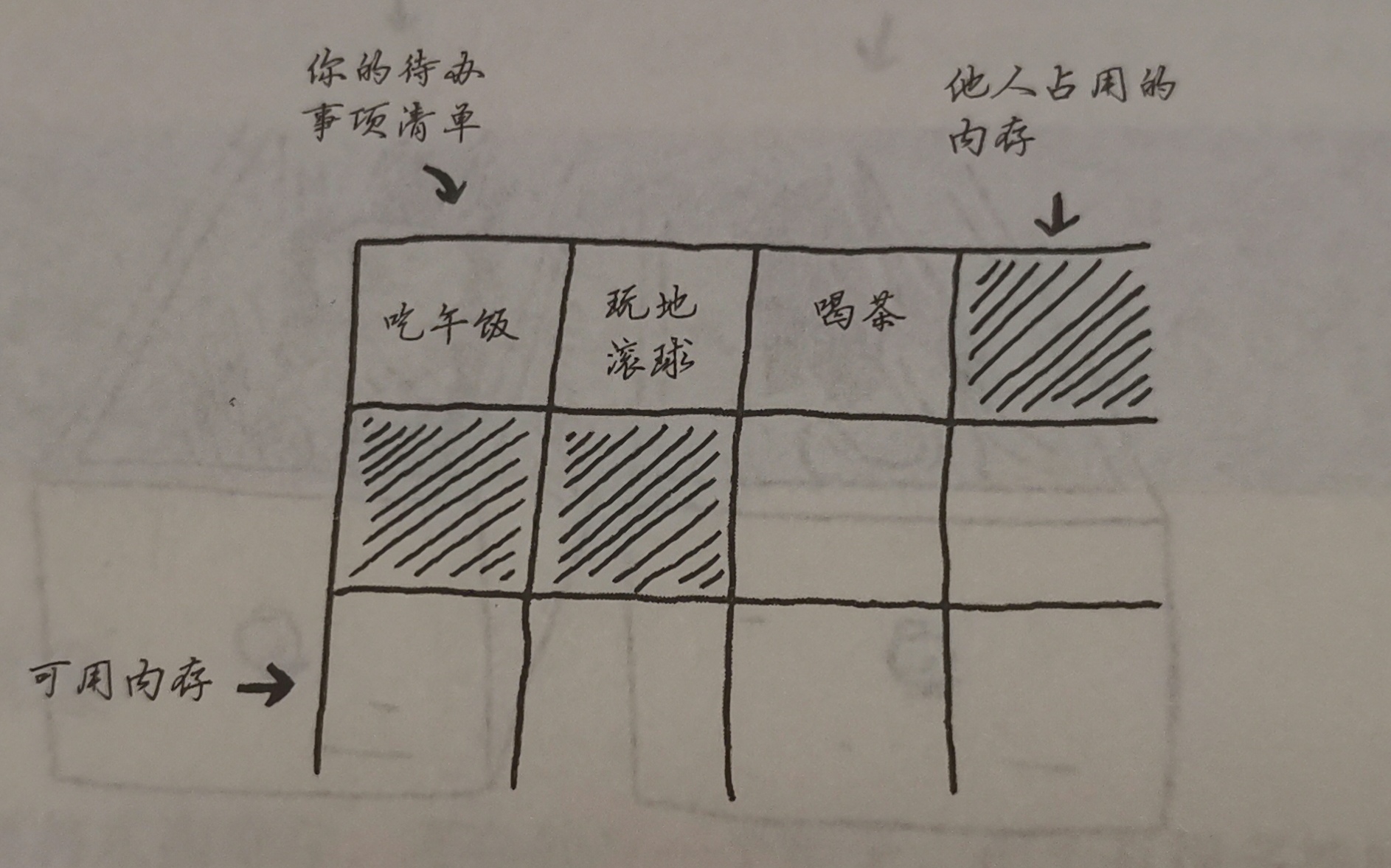
但当多一位需要加入（如和朋友看电影，周围坐满了，但又来了一个朋友，你们需要换一个地方），全部转移到另一个地方，重新分配，时间较长。

解决方法：预留位置/重新分配位置

缺点：预留位置可能没有数据，浪费；重新分配所花时间较长

于是：

链表

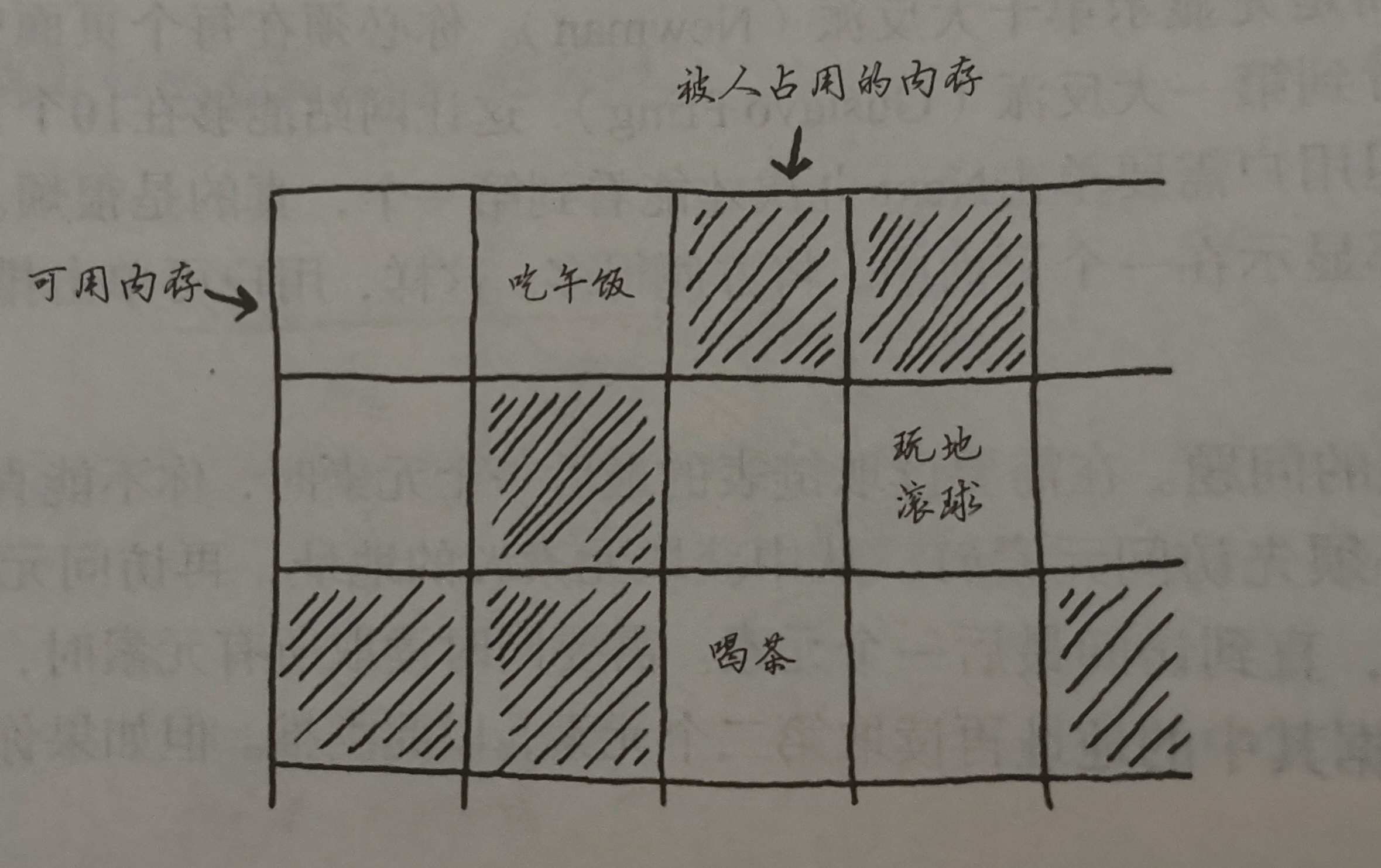
每个元素储存下一个元素的地址

相互分离，但又有联系

不需要移动

数组

一个用于增加网站浏览量的方法：排行榜从10到1，需要多看九页

优点：知道每一个数据的地址，直接访问（链表需要知道第一个然后慢慢推）

术语

value	10	20	30	40
index	0	1	2	3

remember : index stars from 0

	数组	链表
output	O(1)（常量时间）	O(n)（线性时间）
input	O(n)	O(1)
delete	O(n)	O(1)

插入删除数据

链表：

数组：

删除同理

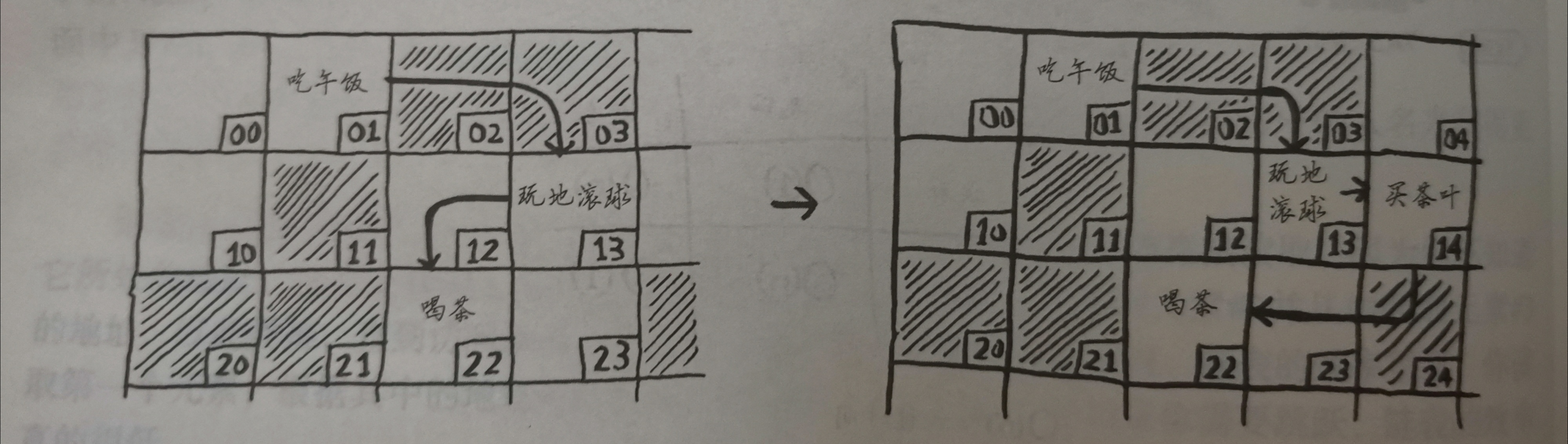
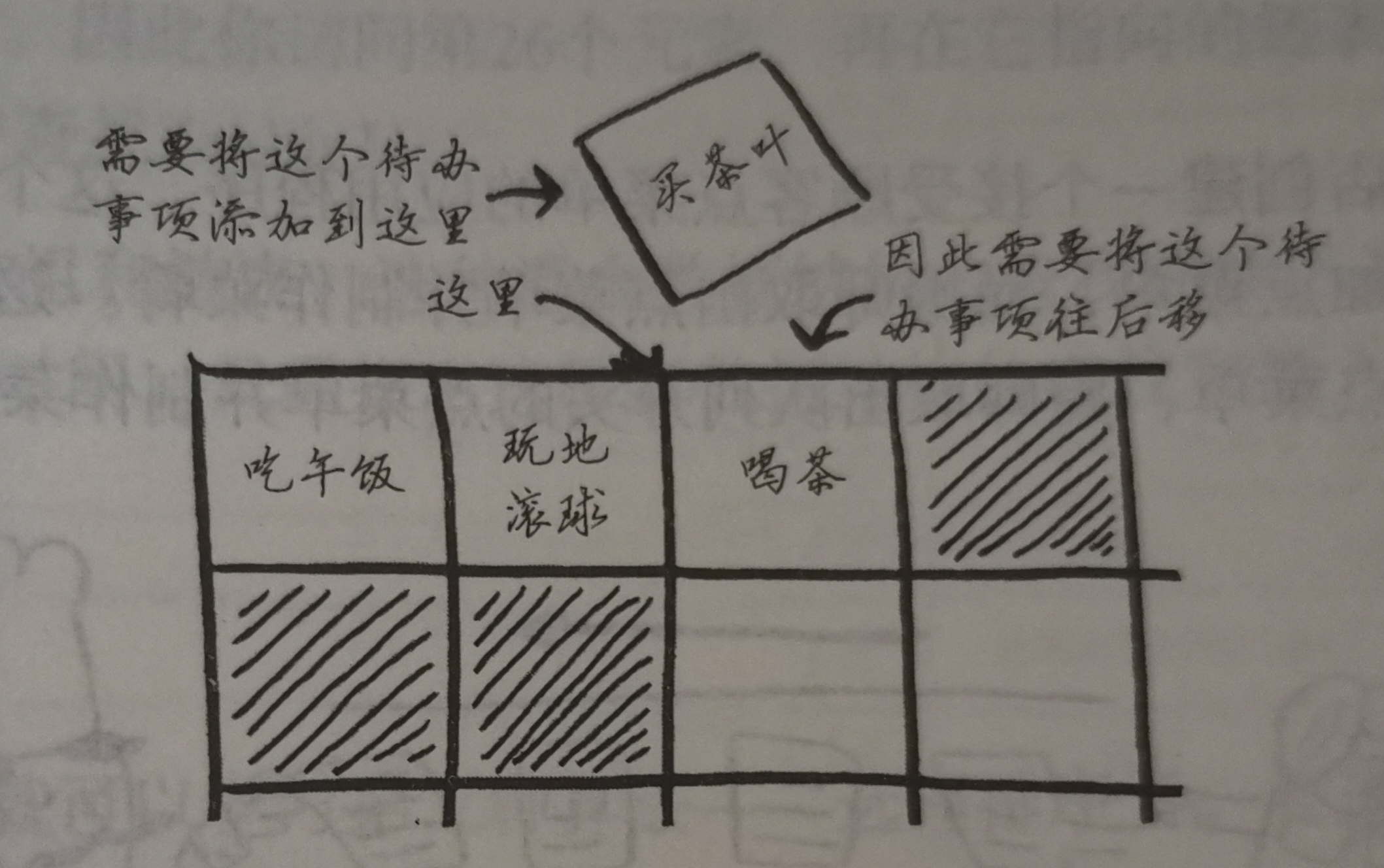
选择排序

将歌曲按播放量排序：

依次找出最多播放量的歌，移入另一个列表

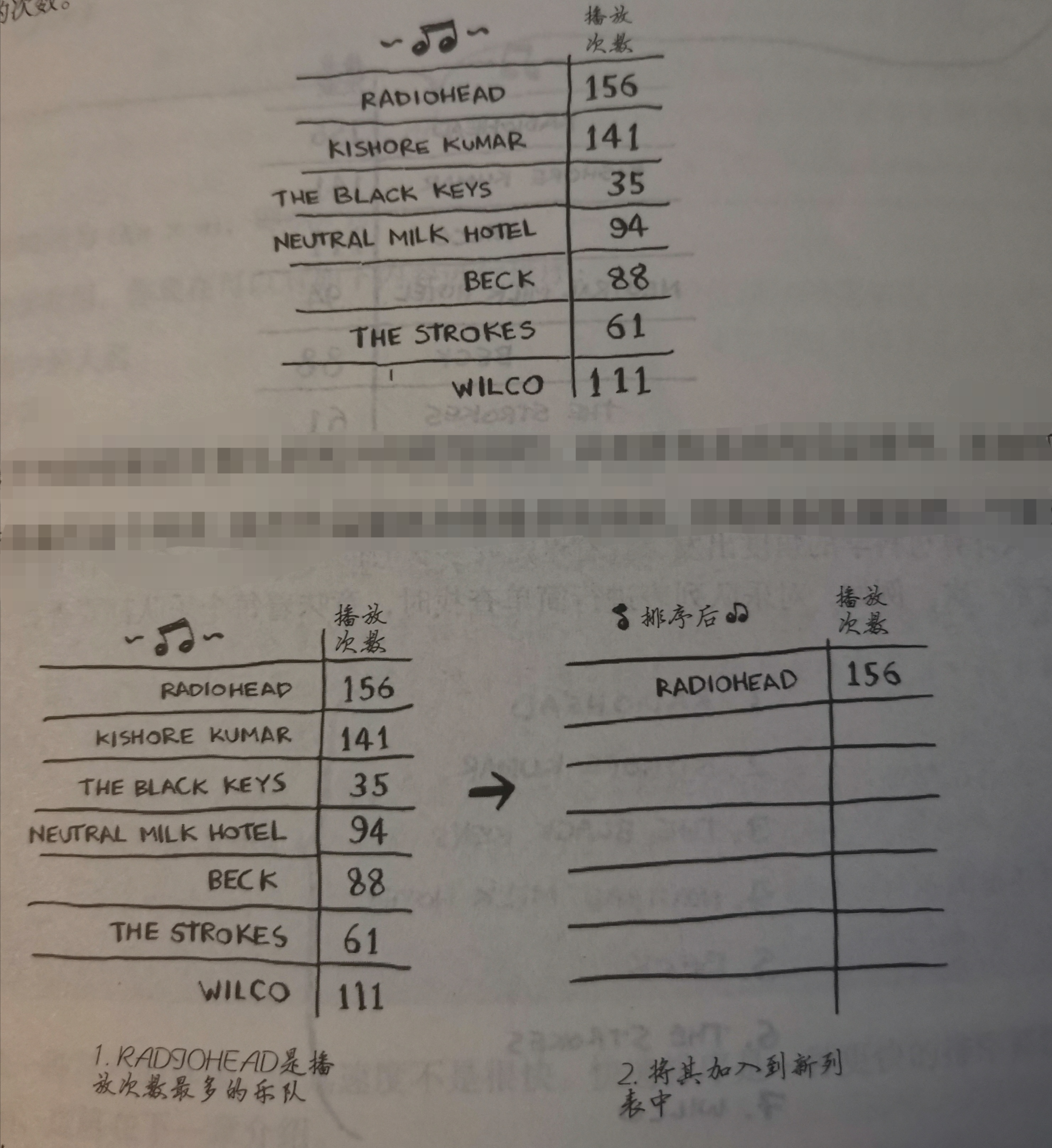
每一次都要运行n次（n指每一个循环的数量而非总数，n在减少）

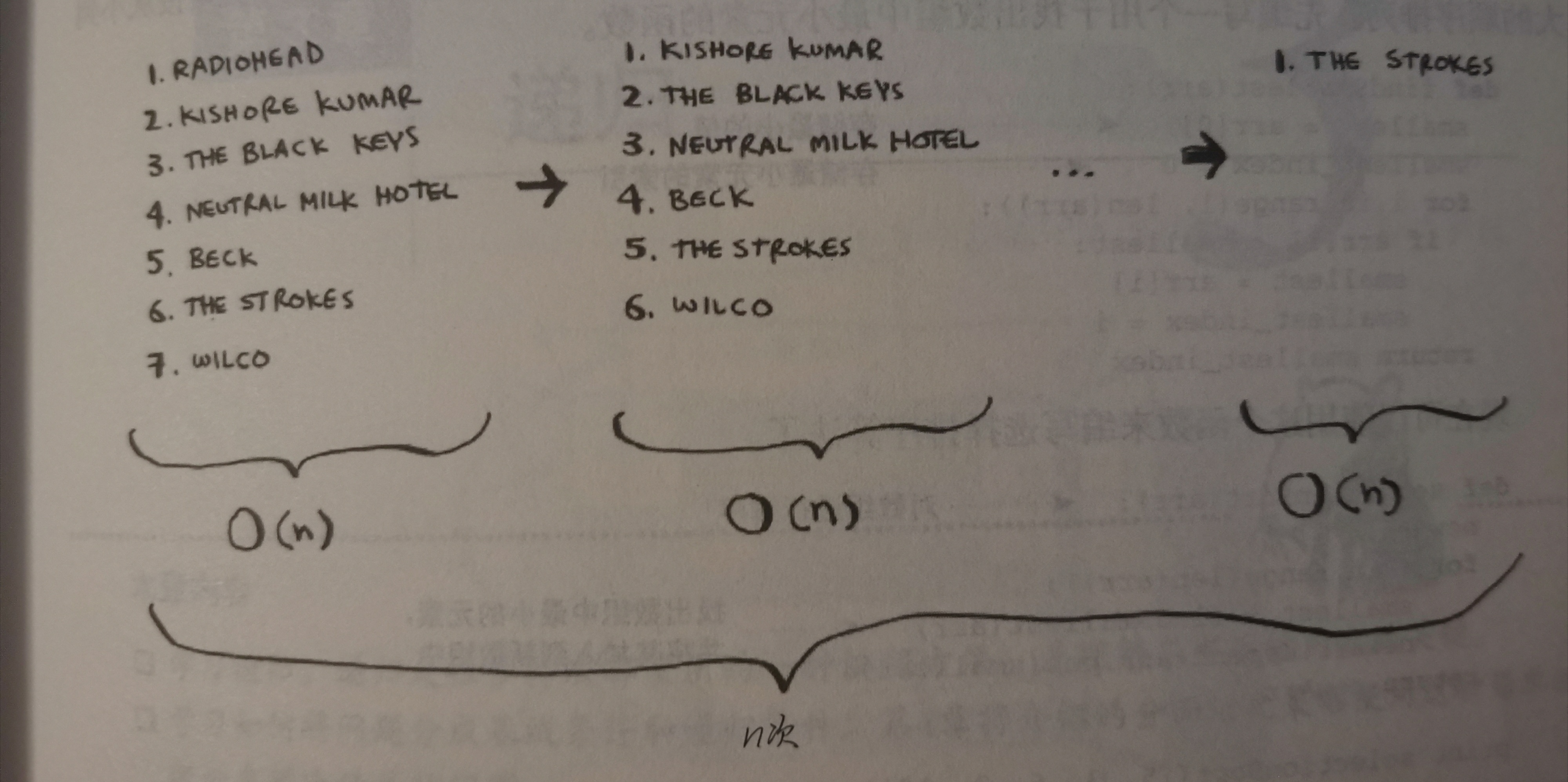
总共有n个数据，则每次需要运行：n-1,n-2,n-3… …2,1

和：(n-1+1)n\1/2=1/2n^2

而大O写法省略1/2（详见第4章）

示例代码：

def findSmallest(arr): #arr=array
    smallest=arr(0)  #储存最小值（如果第一项即为最小值）
    smallest_index=0 #最小值位置
    for i in range(1,len(arr)):
        if arr[i]<smallest:
            smallest=arr[i]  #如果这一项比之前的最小值小，就更换最小值
            smallest_index=i
        return smalest_index
def selectionSort(arr):
    newArr=[]
    for i in range(len(arr)):
        smallest=findSmallest(arr)     #找到最小值
        newArr.append(arr.pop(smallest))  #将最小值放入新列表，删除此最小值
    return newArr

print selection([5,3,6,2,10])

第三章递归

理解递归：

在一个盒子里找钥匙，盒子里还有其他盒子,钥匙可能在盒子里的盒子里

有两种思路：

1.while循环：只要盒子不空、没找到钥匙就继续取

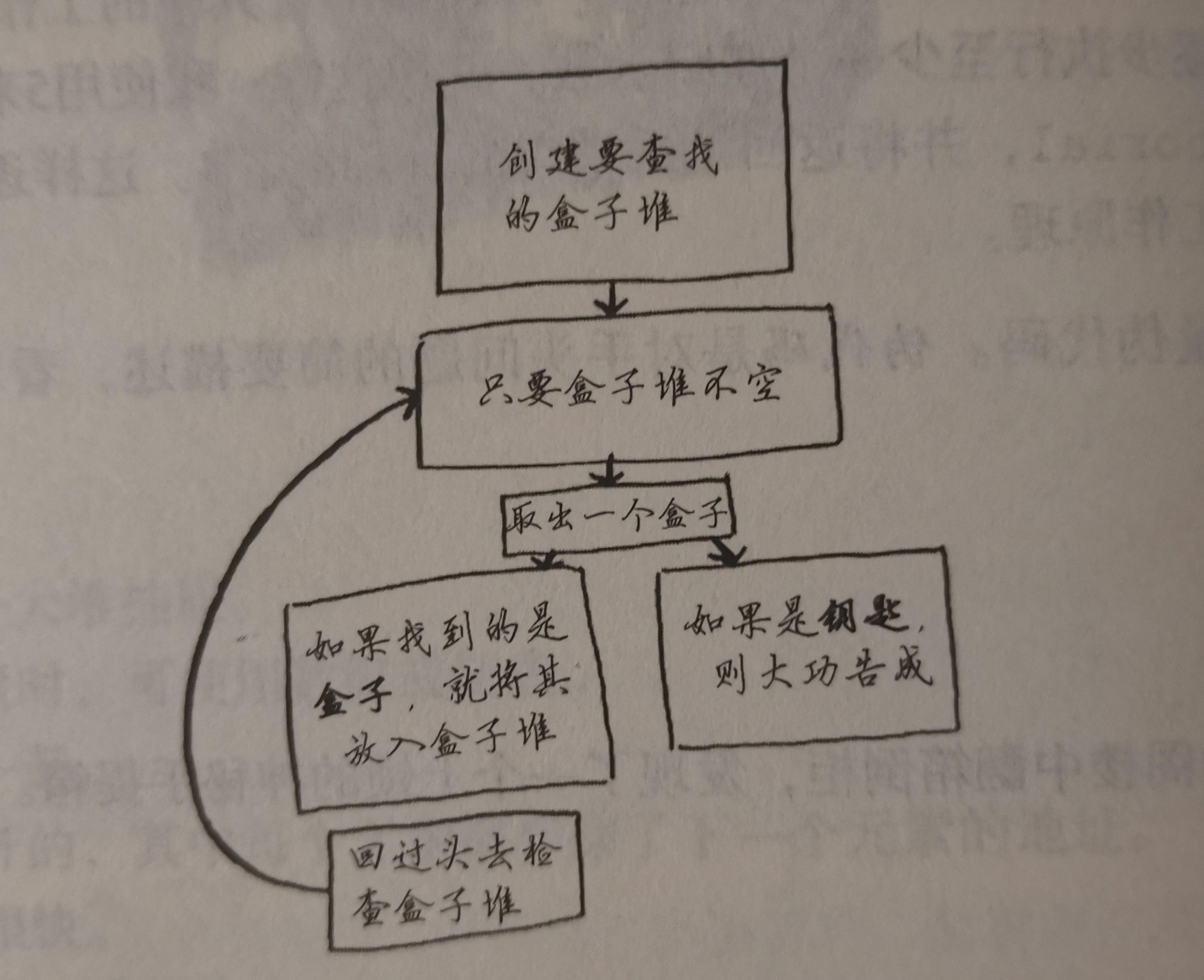
创建盒子堆

在大盒子里取出一个小盒子

如果没有，放入盒子堆

如果有钥匙，结束

不是回到第二步

2.for循环：找到钥匙即结束

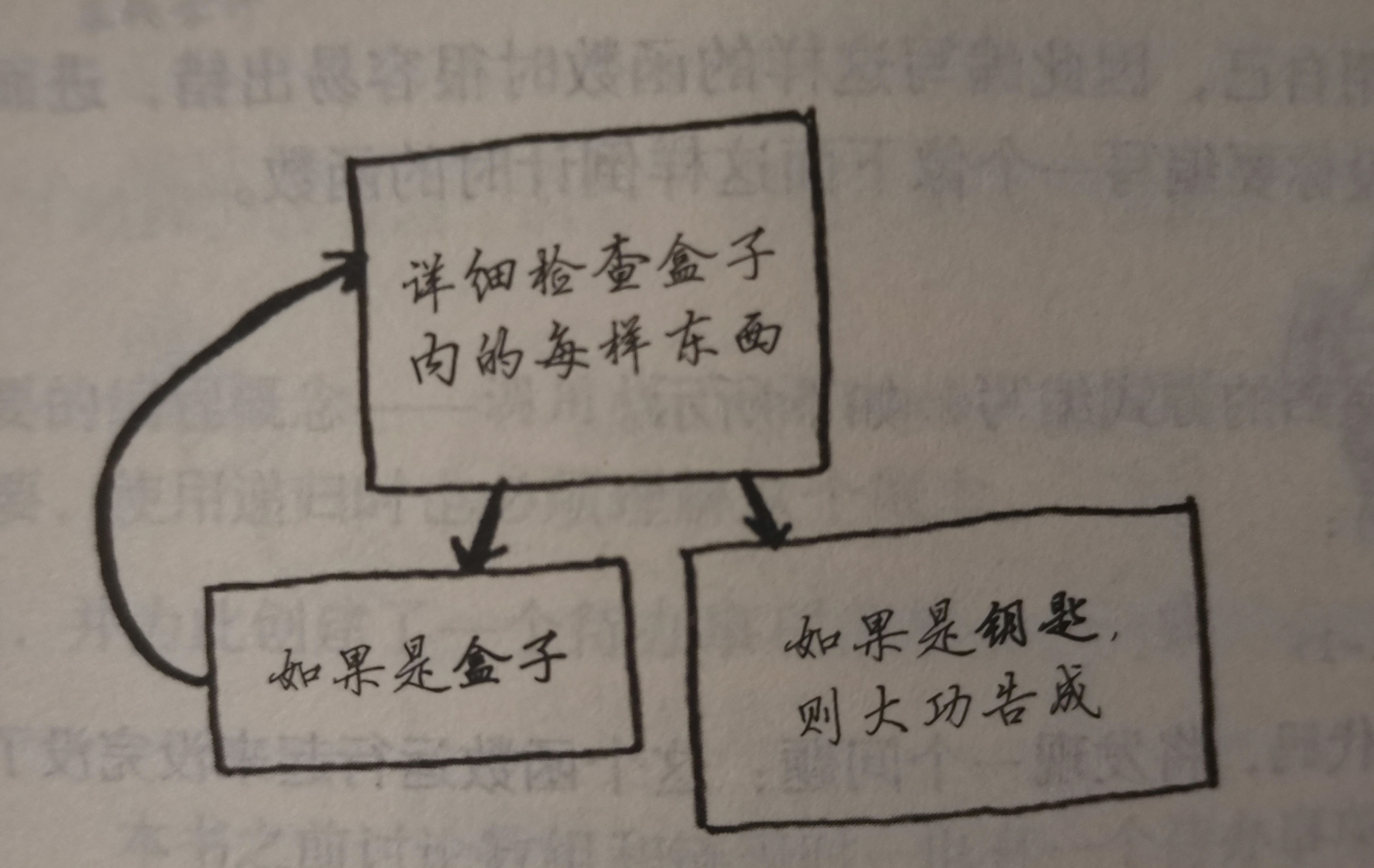
检查每个物品

如果是盒子回到第一步

如果是钥匙结束

伪代码：

def look_for_key(box):

for item in box:

if item.is_a_box():

look_for_key(item) ——>递归，用了自己本身的函数

elif item.is_a_key():

print(“Find the key!”)

第二种更清晰

基线条件和递归条件

递归容易出现死循环：

编写倒计时，如3…2…1

1
2
3

def count down(i):
    print(i)
    count down(i-1)

但结果为3…2…1…0…-1…-2…

(Ctrl+C 可停止)

所以要加基线条件：

def count down(i):
    print(i)
    if i<=1:  #基线条件，到1即停
        return
    else:     #递归条件
        count down(i-1)

栈

调用栈（call stack）

一叠便签记录所要做的事，在最上面添加代办事项；阅读并删除最上面的代办事项

调用栈

def greet2(name):
    print("how are you,"+name+"?")
def bye():
    print("ok bye!")


def greet(name):
    print ("hello,"+name+"!")
	greet2(name)
    print("getting ready to say bye...")
    bye()

假设name=”maggie”，即调用greet(“maggie”)，该函数被分配一个区域

name被设置为maggie并存进去，运行greet(“maggie”)

然后调用greet2(“maggie”)，同上此时第2个函数在第一个上面，当打印完“how are you，maggie？”后从函数返回，此时栈顶的内存被弹出。

此时返回到了greet函数层（调用另一个函数时，当前函数暂停并处于未完成状态），函数值还在内存中，继续运行bye函数。

greet函数用于储存多个函数的变量，被称为调用栈。

递归调用栈

阶乘：fact为调用栈

def fact(x):
    if x==1:
        return 1
    else:
        return x*fact(x-1)

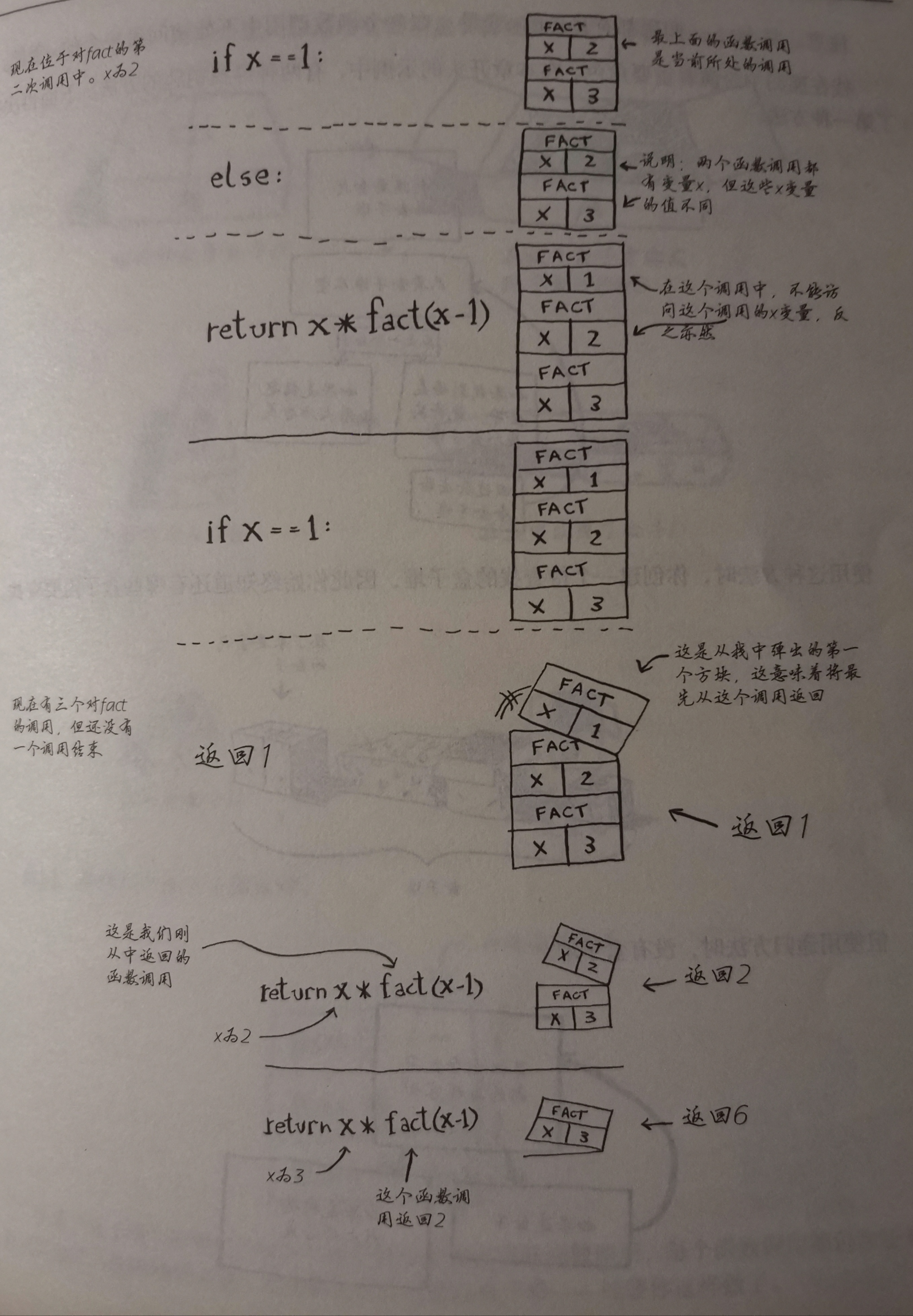
回到开始的盒子找钥匙问题

第一种循环有盒子堆，就始终知道哪些盒子要查

那递归法的盒子堆呢？

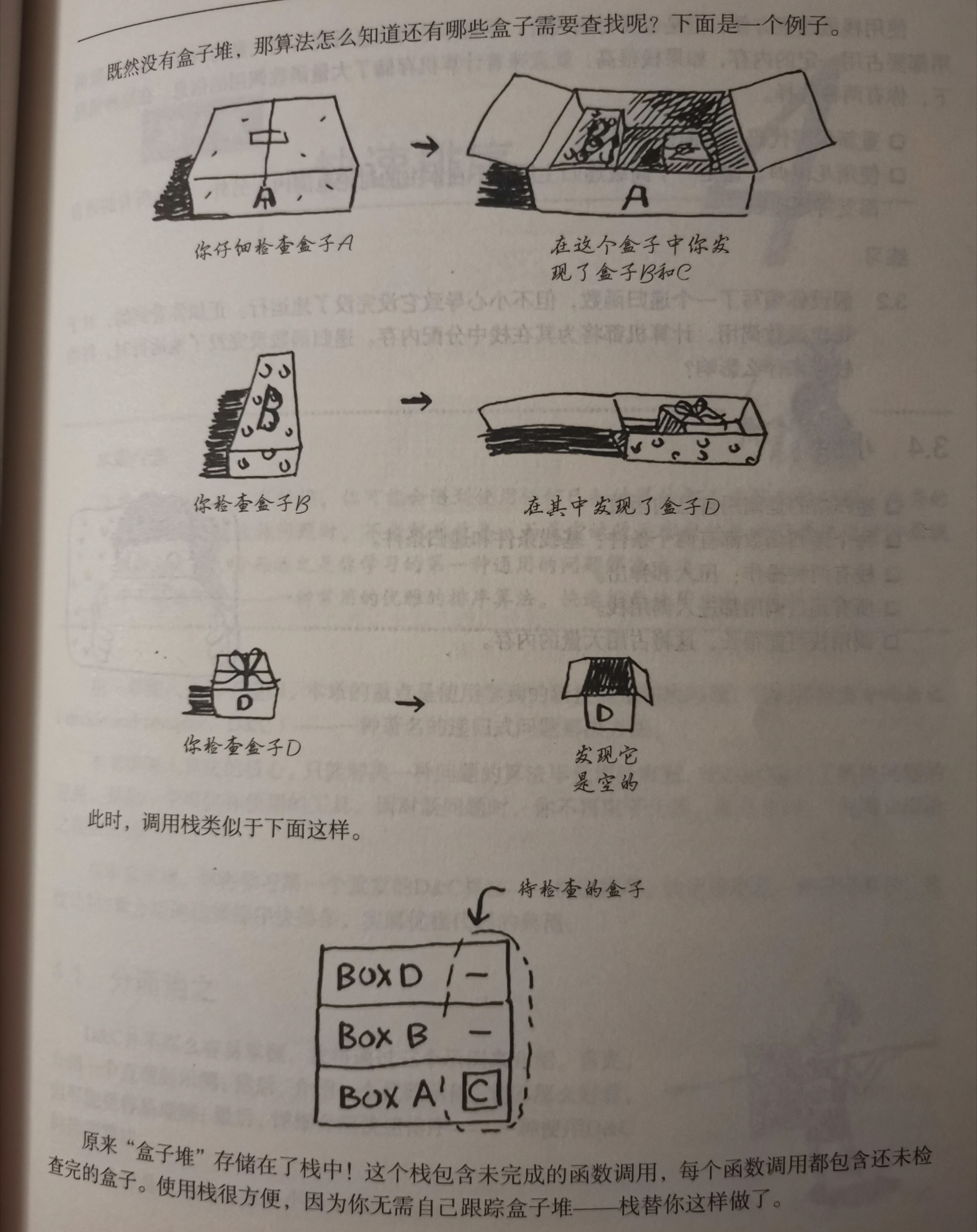
虽然栈很方便，但需要大量的内存